LA DISTRIBUCIÓN NORMAL

Jorge Dagnino S. ¹

---

Rev. chil. anest. Vol. 43 Número 2 pp. 116-121|https://doi.org/10.25237/revchilanestv43n02.08 PDF|ePub|RIS

---

• Una gran cantidad de fenómenos o variables biológicas, psicológicas o sociales, tienen una distribución Normal.

• La distribución normal es simétrica, la media, moda y mediana coinciden, y es descrita completamente por sus dos parámetros mu (µ) y sigma (σ).

• La distibución normal estándar es aquella que tiene una media de 0 y una desviación estándar de 1. El área bajo la curva puede ser calculada por la distancia desde la media; media ± 1,96 DS encierran entre sí el 95% y dejan fuera el 5%, 2,5% a cada lado de la curva.

• El teorema del límite central permite el cálculo del error estándar de la media y el de intervalos de confianza.

Raramente se puede estudiar todo el universo para realizar estudios experimentales u observacionales, por razones prácticas o económicas, por lo que es necesario obtener los datos de una muestra de individuos pertenecientes a esa población. Esa información se usa luego para hacer inferencias sobre esa población, que es lo que generalmente interesa. Sin embargo, la relación entre la muestra y la población es incierta y es necesario estimar esa incertidumbre. Para ello es indispensable tener una idea de las distribuciones de probabilidades teóricas; los modelos de distribución que puede seguir la variable aleatoria de interés. Por variable aleatoria se entiende toda función cuyos valores numéricos se producen al azar, tomando valores variables que tienen diversas probabilidades de ocurrir en una población. Por ejemplo, la estatura de una población es una variable aleatoria, siendo variable (las estaturas son variables y numéricas) y aleatoria pues no se puede predecir cuánto va a medir un individuo que tomemos al azar. A toda tabla, gráfica o expresión matemática que indique los valores que puede tomar una variable aleatoria se le conoce como la distribución de probabilidad de esa variable, si la variable es discreta, o de una densidad de probabilidades si es continua. Estas distribuciones, a pesar de ser teóricas, tienen gran importancia práctica. Matemáticamente los conceptos de distribución de probabilidades y de variable aleatoria están íntimamente interrelacionados: una variable aleatoria tiene una distribución de probabilidades y viceversa.

Afortunadamente, y probablemente por razones no fortuitas, la mayoría de los fenómenos naturales -biológicos, psicológicos o sociales- se ciñen exacta o aproximadamente a unas pocas leyes o distribuciones de probabilidad teóricas siendo cada una de ellas, en realidad, una familia de leyes. Las tres más importantes son las distribuciones: normal, binomial y de Poisson. La primera es de cantidades continuas, las otras dos de discretas. En la preparación de este artículo se incluyeron algunas fórmulas, pensando que ayudan en la explicación, esperando que la aparición de integrales y potencias, muchas “pies y mues”, no predispongan al lector contra el texto. Para disminuir su posible impacto negativo, vale la pena destacar que no es necesaria su memorización y tampoco usarlas en esta era cibernética.

PROBLEMAS DE NOMBRES Y LETRAS

La distribución normal es la más importante por su simplicidad, porque aparece frecuentemente en la realidad y por una propiedad especial llamada Teorema del Límite Central. La comprensión de su naturaleza y su papel en la inferencia estadística es esencial. Es una pena la denominación de normal pues no es más “normal” que las otras y ello causa frecuentes confusiones, sobre todo en medicina, donde normal, es más bien lo que no es patológico. Para evitar la confusión muchos usan Normal con mayúsculas y aquí haremos lo mismo; otros hablan de distribución gaussiana o de campana de Gauss a pesar que fue Abraham de Moivre el primero en describirla y Gauss solo la popularizó.

La distribución Normal:

1. Tiene forma de campana.

2. Es simétrica.

3. Alcanza su máximo en µ (la media).

4. La media es también la moda y la mediana.

5. Es asintótica al eje de las abscisas y, como no lo toca nunca, cualquier valor de X entre -infinito y +infinito es teóricamente posible.

6. La posición relativa en el eje de las abscisas lo determina µ (más a la derecha mientras mayor sea) y su mayor o menor aplastamiento o ancho lo determina σ (la desviación estándar), siendo más aplanada mientras mayor sea su magnitud (Figura 1). Esta característica se denomina curtosis (del griego, curvado): angosta o leptocúrtica (literalmente, curva angosta), media o mesocúrtica y ensanchada o platicúrtica (literalmente, curva ancha) (Figura 2). La altura de la curva carece de importancia o uso en la práctica.

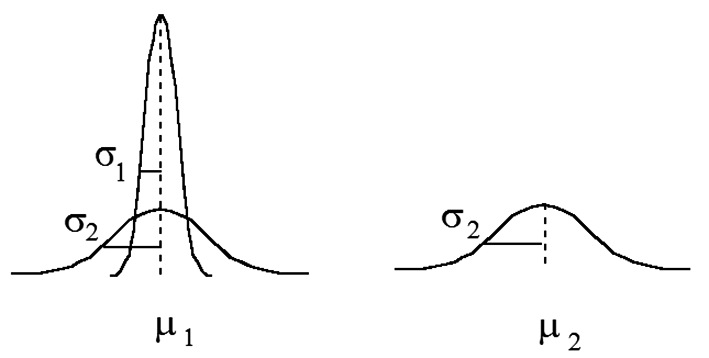
Figura 1 Curvas de distribuciones Normales con igual media y distinta varianza (las dos de la izquierda) y de otras dos con distinta media (µ1 y µ2) e igual varianza (s2) (la izquierda comparada con la derecha). La media µ divide a la distribución en dos mitades y la distancia entre ésta y el punto de inflexión, donde la curva cambia de convexa a cóncava, es el índice de la dispersión de los valores en torno a la media.

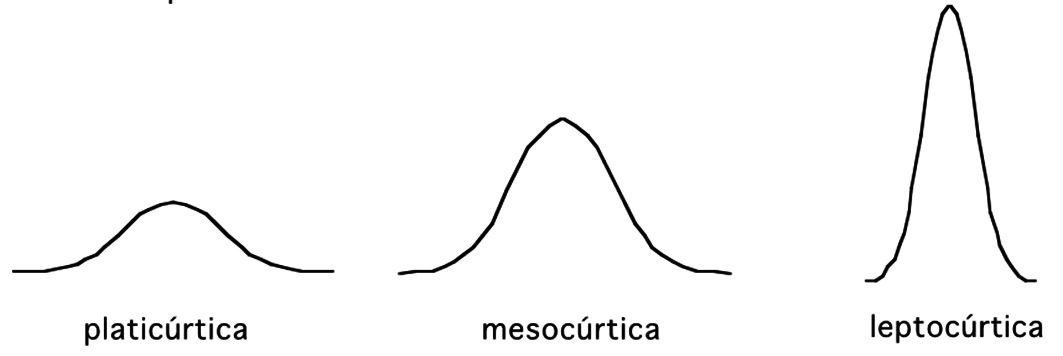
Figura 2 Características de curvas Normales: curtosis.

Las fórmulas para el cálculo de los parámetros poblacionales de la distribución Normal son sencillas:

Mediana:

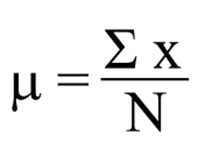
Donde la letra griega Σ, sigma mayúscula, indica la sumatoria de los valores individuales de X, cifra que es dividida por el número de mediciones.

La variabilidad de los valores se calcula como un promedio de las desviaciones con respecto a la media. Como ya vimos, ya que la mitad de los valores son mayores que la media y la otra mitad son menores, el resultado final sería 0. Para eliminar el signo negativo de la mitad menor, se eleva al cuadrado cada desviación. Este promedio de desviaciones elevadas al cuadrado desde la media es la varianza.

Varianza:

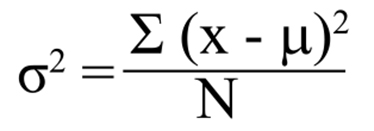
La varianza se expresa con el cuadrado de las unidades de la medición (cm2, kg2, mmHg2) y, además, es más difícil de visualizar e interpretar por el hecho de ser un cuadrado. Por ello es más común que se use la desviación estándar: la raíz cuadrada de la varianza.

Desviación estándar:

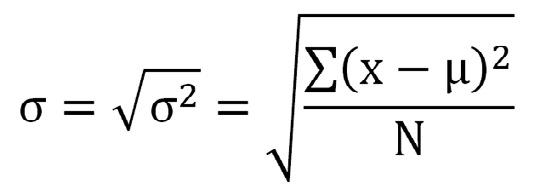
Cada valor en el eje de las ordenadas en relación con cada valor en el eje de las abscisas puede ser calculado con esta ecuación que describe la curva Normal completa:

Curva Normal:

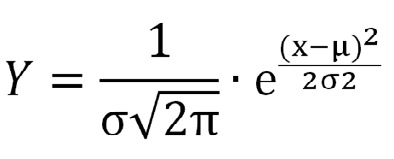
Esta fórmula indica que solo se necesita conocer los valores de µ y σ, o bien buenas estimaciones de ellos como veremos luego, para calcular el valor de Y ante cualquier valor de X.

DISTRIBUCIÓN NORMAL ESTÁNDAR O TÍPICA

Si pensamos que la distribución Normal es una distribución de probabilidades o, más propiamente, una densidad de probabilidades, el área bajo la curva es igual a uno y como es una distribución simétrica, la mitad del área está a la izquierda de la media y la otra mitad a la derecha. Para calcular las probabilidades en relación a cualquier valor de X basta con calcular el área:

Área bajo la curva normal:

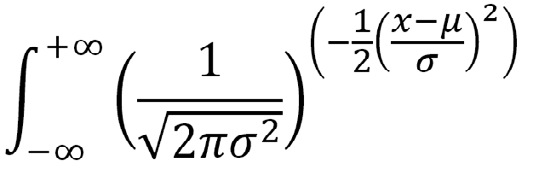
Hay tablas, que aparecen en el apéndice de todos los libros de estadística, en las cuales se ha hecho esta integración. Como cada variable observada tiene valores individuales de X, probablemente todos diferentes y expresados en unidades de medición distintas, sería necesario disponer de tablas o calcular separadamente para cada valor. Sin embargo, pueden ser puestas en una escala comparable usando equivalentes estandarizados. Como se vio, cualquier posición en el eje horizontal puede ser descrita como una distancia expresada en desviaciones estándar desde la media con valor negativo o positivo. Esta unidad se conoce como desviación Normal estándar o puntaje z. Es equivalente a una distribución Normal con una media de 0 y una desviación estándar de 1, una distribución Normal especial conocida como Normal estándar o Normal típica.

La transformación requerida es:

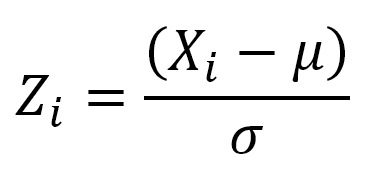
donde Xi es un número observado de una variable distribuida Normalmente con una media µ y una desviación estándar σ.

La ecuación de la curva Normal adquiere una forma más simple al usar z en vez de X:

Área bajo la curva Normal estándar:

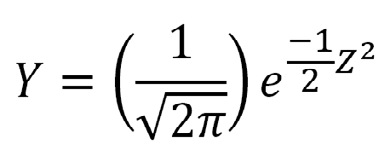
En las tablas de z, se pueden leer las proporciones en que esa área total es dividida en dos por un valor de z. Con ellas podemos calcular la proporción de personas o de valores que esperamos tengan cifras por sobre o por debajo de un valor determinado. Por ejemplo, valores de presión arterial media, variable que se distribuye normalmente en una población, para la cual estimamos valores de µ y σ de 100 y de 15, y queremos saber qué proporción de la población esperamos tengan valores ≤ 120. Usando la fórmula anterior:

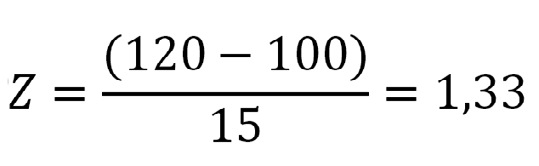
Este valor de z corresponde a una proporción de 0,9082 (Figura 3): estimamos que el 90,82% de la población tiene una PAM ≤ 120.

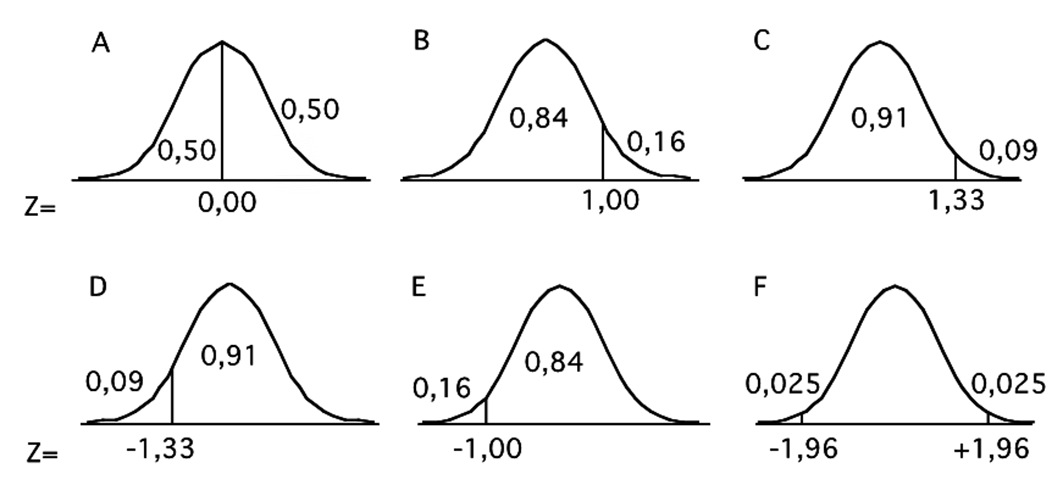
Figura 3 Curva Normal estándar o típica. Se señalan las proporciones del área bajo la curva por sobre o debajo de distintos valores de z. Como el área bajo la curva es igual a uno, las proporciones indican también probabilidad. Nótese que para valores negativos de z sólo es necesario contar el límite hacia la izquierda de la media (D y E que corresponden al valor negativo de z en B y C). También se puede observar en F que valores de z de + 1,96 o de -1,96 separan áreas del 2,5% del total. Este detalle tiene especial importancia a la hora de discutir la inferencia estadística, los valores de p y la significación estadística.

ESTIMACIONES DE µ y σ

Hemos dicho que buena parte de la estructura teórica de la bioestadística y sus cálculos matemáticos se basa en la existencia de poblaciones con una distribución teórica conocida y que para cualquier variable existen valores que se denominan parámetros. Estos raramente se conocen en su real dimensión por lo que nos conformamos con estimaciones de ellos a través de los cálculos hechos con los valores obtenidos en una muestra. Los primeros, los parámetros de una población, son denominados con letras griegas; los segundos, parámetros calculados en la muestra, con letras romanas. Así es una estimación de µ y s una estimación de σ. Mientras más grande es la muestra por la cual se calcularon estas estimaciones, más cercanas serán a los verdaderos parámetros.

Las fórmulas para calcular y s son ligeramente distintas:

Media de la muestra:

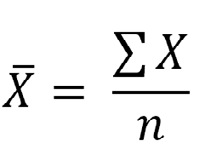
Varianza de la muestra:

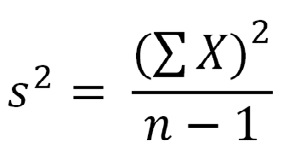
Desviación estándar de la muestra:

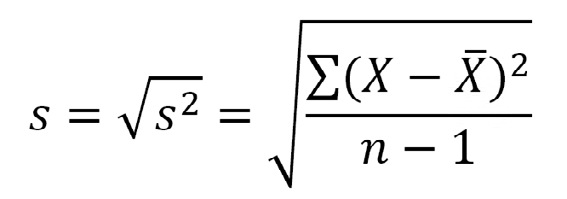
Vale la pena notar algunos cambios además de los señalados. En vez de N, el tamaño de la población, se escribe n para referirse al tamaño de la muestra. Además, en las fórmulas de variabilidad, varianza y desviación estándar, la media de la población ha sido substituida por su estimación en la muestra y el promedio se calcula dividiendo por n-1 en vez de simplemente por n. Esto, que puede causar confusión, no es otra cosa que la compensación por el hecho que la estimación de la variabilidad siempre tiende a subestimar aquella de la población.

ERROR ESTÁNDAR Y TEOREMA DEL LÍMITE CENTRAL

La media de una muestra aleatoria es improbable que sea idéntica a la media de la población. Si bien es la mejor estimación que tenemos, y la única, es indispensable tener una manera de evaluar cuan buena es esa estimación. Una aproximación es suponer que podríamos obtener una serie grande de muestras aleatorias de un determinado tamaño de esa población. Matemáticamente se conoce como el teorema del límite central, y se puede demostrar que la distribución de las medias de esas muestras tienen las siguientes características:

1. La distribución de todas las medias de las muchas muestras tomadas es Normal si la distribución de los valores en la población es Normal. Además, la distribución de las medias de las muestras será aproximadamente Normal, no importando cual sea la distribución de la variable en la población, siempre que las muestras sean suficientemente grandes.

2. El promedio de las medias de todas las muestras posibles es igual a la media de la población.

3. La desviación estándar de las medias de las muestras, que se conoce como el error estándar de la media, depende de la variabilidad de la población y del tamaño de las muestras.

Error estándar:

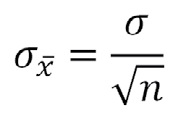
Como no conocemos σ, usamos la desviación estándar de la muestra para una estimación del error estándar:

Estimación del error estándar:

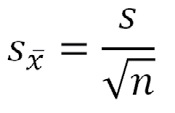
Se puede también calcular los límites de confianza de la estimación de la media:

Límites de confianza:

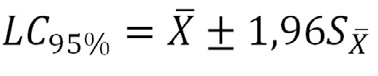
Esto es, esperamos, con un 95% de confianza de estar en lo cierto, que la media de la población estará dentro de 1,96 errores estándar por sobre o debajo de la media de nuestra muestra. Es evidente que mientras mayor sea el tamaño de la muestra, más pequeño es el error estándar y menor el rango entre los límites de confianza.

Se debe recalcar que el error estándar no es una medida de la variabilidad de la muestra y no debe ser usado con ese fin. Este es uno de los errores más frecuentemente detectados en la literatura médica, ya sea por ignorancia o premeditadamente para dar la impresión de una menor imprecisión de las estimaciones.

 

TRANSFORMACIONES HACIA UNA DISTRIBUCIÓN NORMAL

El coeficiente de sesgo o bies es una medida de la simetría. Una distribución simétrica tiene un coeficiente igual a cero. Una distribución sesgada hacia la izquierda, lo más frecuente, tiene un coeficiente positivo y una desviada hacia la derecha tiene un coeficiente negativo. Para valores que no pueden ser negativos, se puede inferir que una distribución es sesgada cuando la desviación estándar es mayor que la mitad de la media. Lo contrario no es necesariamente así, pero un histograma revelará rápidamente cuándo una distribución es sesgada. Una posibilidad de describir una población sesgada es usar parámetros distintos que los de una distribución Normal simétrica, generalmente la mediana y percentiles y para la inferencia se usarán pruebas no paramétricas. Otra alternativa es usar una transformación de los datos de manera que tengan una distribución más simétrica. La transformación más frecuente es la de obtener logaritmos de los datos. El antilogaritmo de la media aritmética de los valores transformados es la media geométrica. Si la transformación fue exitosa en eliminar el sesgo, la media geométrica será similar a la mediana y algo menor que la media aritmética de los datos originales. No tiene sentido obtener el antilogaritmo de la desviación estándar de los valores transformados. No se debe asumir que una distribución sesgada puede hacerse más simétrica con una transformación como la mencionada por lo que debe comprobarse el efecto mirando un histograma de los datos transformados o bien con pruebas como la W de Shapiro-Wilk.

REFERENCIAS

1. Altman DG, Bland JM. Statistics notes: Detecting skewness from summary information. BMJ 1996; 313: 1200.
2. Altman DG, Bland JM. Statistics notes: Quartiles, quintiles, centiles, and other quantities. BMJ 1994; 309: 996.
3. Altman DG, Bland JM. Statistics notes: The normal distribution. BMJ 1995; 310: 298.
4. Altman DG, Gore SM, Gardner MJ, Pocock SJ. Statistical guidelines for contributors to medical journals. Br Med J 1983; 286: 1489-1493.
5. Altman DG. Practical Statistics for Medical Research. London: Chapman&Hall,1991.
6. Bland JM, Altman DG. Standard deviations and standard errors. BMJ 2005; 331: 903.
7. Bland JM, Altman DG. Statistics notes: Logarithms. BMJ 1996; 312: 700.
8. Bland JM, Altman DG. Statistics notes: Transforming data. BMJ 1996; 312: 770.
9. Bland M. An Introduction to Medical Statistics. 3rd Ed: Oxford: OUP, 2006.
10. Feinstein AR. On central tendency and the meaning of mean of pH values. Anesth Analg 1979; 58: 1-3.
11. Glantz SA. Primer of Biostatistics. 3a edición, New York: McGraw-Hill, 1992.
12. Portney LG, Watkins MP. Foundations of Clinical Research. Applications to practice. 2nd ed., Upper Saddle River: Prentice-Hall, 2000.