Correlación

Jorge Dagnino S. ¹

Rev. chil. anest. Vol. 43 Número 2 pp. 150-153|https://doi.org/10.25237/revchilanestv43n02.15 PDF|ePub|RIS

• El coeficiente de correlación r de Pearson mide el grado de asociación lineal entre dos variables.

• El valor de r puede situarse entre -1 y +1. La prueba de significación se hace con la hipótesis nula de que no hay asociación, r = 0.

• Deben calcularse y comunicar los intervalos de confianza de r.

• Antes de decidir la aplicabilidad de una correlación lineal se debe siempre graficar en una “nube de puntos” la relación entre las dos variables.

• Las alternativas no paramétricas son los coeficientes de correlación de Spearman (rho – ρ) o de Kendall (tau – T).

• Existen numerosos errores en la aplicación de la correlación ante los que el lector debe estar alerta.

Muchas veces, cuando se miden dos variables que cambian en conjunto, no es posible determinar cuál es la independiente o cual la dependiente. En estas circunstancias, sólo es posible describir la fuerza de la asociación entre ellas ya que no se puede hacer predicciones o estimaciones causales. Cuando las variables son cualitativas, el modo de determinar si están relacionadas es a través de una tabla de contingencia y, de estarlo, medidas de la fuerza con que se relacionan son, por ejemplo, la razón del producto cruzado o el riesgo relativo. Cuando las variables son cuantitativas, el modo de determinar si están relacionadas o no es a través de la regresión lineal y, de estarlo, una medida de la fuerza con que están relacionadas es el coeficiente de correlación lineal. En este capítulo se describe este último, el coeficiente de correlación de Pearson para datos paramétricos y el de Spearman y el de Kendall, de rangos, para datos no paramétricos.

COEFICIENTE DE CORRELACIÓN LINEAL DE PEARSON

En el artículo sobre regresión lineal se desarrolló el concepto de que la variabilidad total en la relación entre dos variables tenía dos partes: por un lado la variabilidad total de Y y por otro la variabilidad de Y que la variable X es capaz de explicar. Se vio que el coeficiente de determinación es una buena medida de esa capacidad que tiene X para predecir Y:

Coeficiente de determinación:

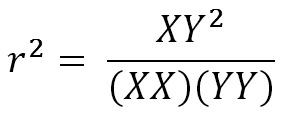
Como la ecuación es simétrica en ambas variables, mide indistintamente la relación de X con Y y también de Y con X (r_xy y r_yx). Además, las dimensiones del numerador se cancelan con las del denominador por lo que el número resultante es adimensional y no es afectado por las unidades de medida. Por otro lado, conceptualmente, r2 es la fracción de la variabilidad de Y que queda explicada por su dependencia de la variable X. Así, un coeficiente de determinación de 0,64 significa que de la variabilidad total de Y, un 64% se explica por su relación con X y el resto por otros factores desconocidos. Sin embargo, esto puede prestarse a confusión por el vocablo, ya que una línea de regresión estrictamente explica nada, en una forma mecanística, entre las variables.

Como r2 no contiene información respecto del signo de (XY), que es fundamental pues es el signo de la pendiente, se define como coeficiente de correlación lineal simple o coeficiente de correlación de Pearson a su raíz cuadrada:

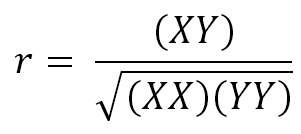
coeficiente de correlación r es una cantidad que puede ser negativa o positiva que va de 0 a -1 o de 0 a +1. Cero indica ausencia de relación y mientras más cerca de 1, sin importar el signo, mayor es la fuerza de la asociación entre X e Y. En esencia, r mide la dispersión de los puntos en torno a una tendencia lineal subyacente.

El coeficiente de correlación se puede calcular para cualquier grupo de datos. Sin embargo, para usar las pruebas de hipótesis es indispensable que al menos una de las variables tenga una distribución Normal. Para que el cálculo de los intervalos de confianza sea válido, ambas variables deben seguir una distribución Normal. En la práctica, entonces, para usar el coeficiente de correlación de Pearson es preferible esta segunda situación, el que ambas variables tengan una distribución Normal. La mejor manera de chequear la validez del uso del test de hipótesis es haciendo un gráfico con los puntos obtenidos y observar su distribución.

Datos de este tipo generan una nube de puntos elíptica en la que el grado de elongación de la elipsis se relaciona con la magnitud del coeficiente de correlación. Este patrón puede ser difícil de detectar en casuísticas pequeñas. Si los datos no tienen una distribución Normal, una o las dos variables pueden ser transformadas, observando nuevamente la nube de puntos que generan. En la Figura 1, se grafican los valores de X e Y en nubes de puntos y se puede ver varias alternativas y sus correspondientes valores de r. Mientras más cerrada es la nube, mayor es el valor de r.

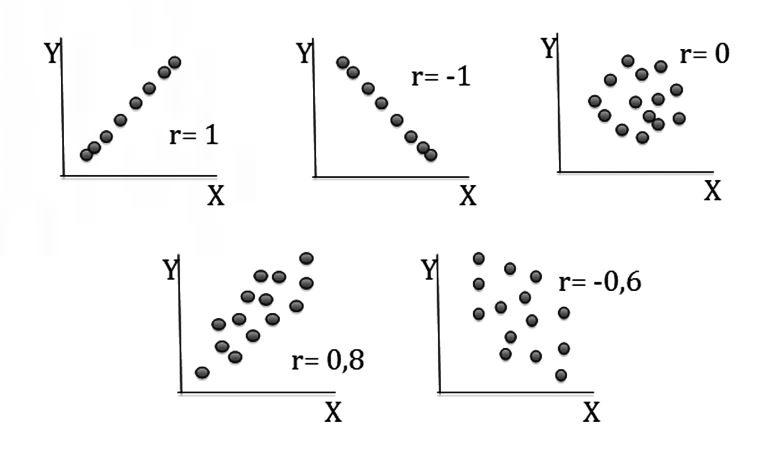
Figura 1 Nubes de puntos y fuerza de la asociación entre las dos variables.

No debe perderse de vista que r es en realidad un coeficiente de correlación muestral y que el valor obtenido en otra muestra seguramente será diferente. Rho (ρ) es el coeficiente de correlación poblacional, un parámetro (y que no debe confundirse con el estadístico rho de Spearman). De nuevo, aquí vale la pena repetir el concepto de que r es la mejor estimación muestral que tenemos del valor del parámetro poblacional ρ. Los intervalos de confianza son de vital importancia para juzgar la incertidumbre envuelta en la estimación hecha con r ya que aisladamente la magnitud de este no permite juzgar enteramente su valor. Con muestras escasas, correlaciones bastante por sobre 0,9 pueden estar asociadas a considerable incertidumbre.

El otro problema es cuantificar la probabilidad con que el r obtenido difiere de cero, la hipótesis nula de que no hay asociación entre las variables. El valor del estadístico es:

de donde queda claro que un valor pequeño de n es crítico en determinar un valor pequeño del estadístico y que un n grande causa lo contrario (Figura 2). Si los límites de confianza 95% calculados para r incluyen el cero, se puede concluir que p será > 0,05.

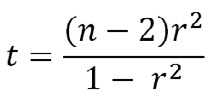
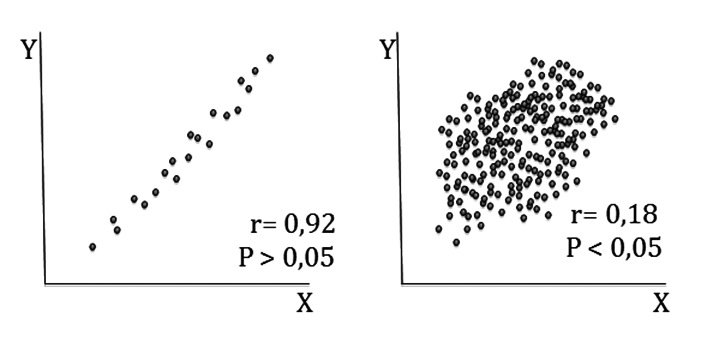
Figura 2 El hecho que r alcance significación estadística, es decir que sea diferente de cero, depende del tamaño de la muestra. Muestras pequeñas con r grandes pueden no alcanzar significación; a la inversa, muestras grandes con r pequeños pueden alcanzar significación estadística aunque no la tengan clínicamente. En la figura la fuerza de la asociación es ostensiblemente mayor en la figura de la izquierda (“no significativa”) y menor en la de la derecha (“significativa”).

INTERPRETACIÓN, USOS Y ABUSOS

La interpretación del coeficiente de correlación casi siempre exige información adicional, más allá del simple número y de la p asociada. Un coeficiente de 0,7 puede ser importante o no dependiendo de las circunstancias. En cualquier caso, no está de más recordar que, al igual que la regresión, una correlación significativa jamás es prueba de causalidad. Además de la restricción en cuanto a la distribución de los datos, otra limitación en el uso de r es que las dos variables deben ser independientes y que sólo una observación de cada variable debe venir de cada individuo estudiado. Aun si las presunciones mencionadas no son violadas, el uso del coeficiente de correlación no es tan simple como parece. El mal uso es tan común, que algunos autores han deseado que el método no se hubiese inventado.

He aquí algunos ejemplos de mal uso:

• Usar r de Pearson en asociaciones no lineales: una correlación baja podría llevar a la conclusión que no existe asociación cuando esta puede ser fuerte aunque no lineal. Por ello, siempre debe analizarse la nube de puntos; los autores deben especificar que esta maniobra se hizo antes de decidir qué análisis se usó. En el mismo sentido, algunos valores extremos, “outliers”, pueden alterar mucho el valor de r cuando el tamaño de la muestra es pequeño.

• Dragado de datos: estudios en los que se registran gran cantidad de variables en los que es posible calcular decenas o incluso cientos de r. Por ejemplo, con 10 variables es factible hacer 45 correlaciones y 20 variables pueden originar 190. En estas circunstancias, 1 de cada 20 serán estadísticamente significativos, sólo por azar, y no hay manera de distinguir estas de las verdaderas asociaciones.

• Correlaciones espurias sobre el tiempo: la correlación de dos variables que han sido registradas en forma repetida a lo largo del tiempo puede llevar a conclusiones falsas. Por ejemplo, precio del petróleo y tasa de divorcios, aumento en el número de televisores y disminución de la tasa de natalidad. Hay sitios web con numerosos ejemplos de correlaciones espurias.

• Muestreo restringido de los individuos: cualquier suma o reducción de la muestra puede tener implicancias mayores en la correlación pues la variabilidad entre sujetos entra directamente en el cálculo.

• Uso del coeficiente de correlación para comparar dos métodos de diagnóstico: como miden la misma variable, casi siempre tienen correlaciones elevadas. Sin embargo, el método sólo mide fuerza de asociación y no cuánto coinciden o difieren que es lo que verdaderamente interesa. Para ello se recomienda usar el método de Bland y Altman de concordancia o “agreement”.

• Algo parecido sucede con la correlación entre un valor inicial y sus cambios en el tiempo. En cualquier circunstancia, para dos variables X e Y, X se correlacionará con X-Y, incluso si son números aleatorios. El mismo fenómeno, regresión a la media, se produce cuando se correlaciona una parte con el todo: por ejemplo, altura a los 5 años con altura de adulto, consumo de proteínas con consumo de calorías.

• Muestras mezcladas: la correlación puede confundir cuando la muestra está constituida por subgrupos diferentes. Por ejemplo analizar la correlación entre edad y grasa corporal o edad y estatura mezclando hombres y mujeres.

CORRELACIÓN POR RANGOS: SPEARMAN Y KENDALL

Cuando se tiene sospechas acerca de la normalidad de la distribución es preferible usar un método alternativo para datos no paramétricos. El más conocido es el coeficiente de correlación de Spearman, que se basa en asignar rangos a los valores de las variables en cuestión. El coeficiente de regresión se anota como r_s. o a veces como rho de Spearman. Su cálculo es exactamente igual que el de Pearson, pero sobre los rangos y no los valores absolutos. Su potencia puede ser similar o sólo levemente menor.

Otro coeficiente de rangos, la tau de Kendall, se usa cuando existen múltiples variables independientes. Como coeficiente de correlación parcial, se usa cuando se tienen datos sobre una tercera variable que puede influir sobre la asociación entre otras dos variables de interés. Puede considerarse como la correlación estimada entre esas dos variables con el mismo valor de la tercera variable. Sus conclusiones son idénticas al coeficiente de correlación de Spearman cuando se trata de sólo dos variables.

Referencias

1. Altman DG, Bland JM. Measurement in Medicine: the Analysis of Method Comparison Studies. The Statistician 1983; 32: 307-317.
2. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
3. Bland JM y Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986; I: 307-310.
4. Bland JM, Altman DG. Correlation in restricted ranges of data. BMJ 2011; 342: d556.
5. Bland M, Altman DG. Comparing methods of measurement: why plotting difference against standard method is misleading. Lancet 1995; 346: 1085-1087.
6. Bland M. An Introduction to Medical Statistics. 3rd Ed,, Oxford: OUP, 2006.
7. Feinstein AR. Clinical Biostatistics. Saint Louis: Mosby, 1977.
8. Glantz SA. Primer of Biostatistics. 3a edición, New York: McGraw-Hill, 1992.
9. Guyatt G, Walter S, Shannon H, Jaeschke R, Heddele N. Basic Statistics for Clinicans: 4. Correlation and Regression. Can Med Ass J 1995: 152: 487-504.
10. Kozak M. Including the Tukey Mean-Difference (Bland-Altman) Plot in a Statistical Course. Teaching Statistics 2014; 36: 83-87.
11. Mantha S, et al. Comparing Methods of Clinical Measurement: Reporting Standards for Bland and Altman Analysis. Anesth Analg 200; 90: 593-602.
12. Portney LG, Watkins MP. Foundations of Clinical Research. Applications to practice. 2nd ed. Upper Saddle River: Prentice-Hall, 2000.
13. Smith GD, Ebrahim S. Data dredging, bias, or confounding. They can all get you into the BMJ and the Friday papers. BMJ 2002; 325: 1437-1438.