Pablo O. Sepúlveda V. 1
Rev Chil Anest Vol. 40 Núm. 1 pp. 66-76|doi:
PDF|ePub|RIS
Los modelos farmacocinéticos-farmacodinámicos son instrumentos útiles para representar la realidad, si bien son perfectibles todos son incompletos. Los orígenes metodológicos diversos de los modelos de propofol explican gran parte de las diferencias. La tecnología de la infusión controlada por ordenador (TCI) ha permitido incorporar variables complejas, mejorando la predicción y la validez de su uso a gran parte de la población, simplificando al anestesiólogo el complejo trabajo de calcular los ajustes temporales durante la anestesia. La evolución del estudio del comportamiento de propofol es un gran ejemplo de análisis.
¿Qué es un modelo farmacocinético/farmacodinámico?
El cerebro humano obtiene a partir las distintas aferencias sensoriales y sensitivas la información del medio externo para, luego de integrada y procesada, reaccionar de la mejor forma. Esta reacción es permanentemente reajustada según lo adecuado de la respuesta, afinándola constantemente. En este proceso, producto del aprendizaje, se va creando una imagen (modelo) del medio sobre la cual interactuamos. En anestesiología las decisiones se basan en interpretar señales biológicas muchas veces indirectas, traducidas a nuestros monitores. Esas señales nos permiten crear modelos o algoritmos de interpretación de las señales multiparamétricas que nos orientan a dar una respuesta a la situación clínica.
Un modelo pretende explicar cómo son las cosas o por qué no son lo que queremos, pero a la vez la descripción de la realidad es limitada a nuestros sentidos o a nuestros instrumentos tecnológicos. Por ejemplo: ¿mide el BIS el correlato neural de la conciencia o es sólo una correlación indirecta con estados de sedación?; para conocer la perfusión tisular nuestra acción más común es medir la tensión arterial, pero ésta es una medida indirecta y sólo válida en el contexto de una interpretación con otras señales.
La descripción de la farmacocinética (FC) de las drogas es también un proceso de simplificación de la realidad, que intenta describir la sincronía de los procesos distributivos y de eliminación. Es decir, en base a la matemática trata de explicar un modelo de comportamiento específico para cada droga. Lo complejo es que además el modelo es dinámico, y es diferente en distintos escenarios metodológicos y para diferentes poblaciones.
Es común que la construcción de estos modelos se realiza en ambientes controlados, diferentes de la condición clínica (generalmente cambiante), además se realiza en poblaciones sanas y que representan parcialmente a un paciente que viene a recibir anestesia. Eso ha obligado a un trabajo de optimización progresivo que, luego de haber construido los modelos más básicos, avanza, agregando a cada modelo más covariables de ajuste (ej. edades extremas, relación peso-talla, sangrado, cambios en débito cardíaco, etc.) y en generar condiciones que amplíen la descripción de la FC, lo más cercanas a las variadas condiciones de trabajo clínico.
Propofol, el hipnótico más usado en este momento en anestesia, ha sido el prototipo más utilizado para el desarrollo de modelos farmacológicos y ha permitido desarrollar un inmenso cúmulo de información conceptual en cómo se comportan las drogas en su proceso distributivo y de eliminación.
Propofol tiene algunas complejidades particulares, como su gran liposolubilidad (mayor a la de los gases halogenados) 1 , pero gran aclaramiento y una instalación del efecto relativamente rápida y predecible. A la vez tiene dificultades en la descripción de la cinética porque tiene un impacto hemodinámico moderado que produce per se cambios en las concentraciones plasmáticas. Otras complejidades, como el atrapamiento pulmonar en pacientes jóvenes o si se usan velocidades altas de perfusión durante la inducción, hacen que la descripción del proceso sea de alta complejidad 2 , 3 .
A la farmacodinamia del propofol le ha sucedido algo similar en lo que respecta a la descripción del curso temporal de la instalación y desaparición del efecto, representado en el denominado ke0, y a la definición de las concentraciones útiles de trabajo clínico (EC50-95).
Después de un bolo inicial, la infusión que se administre debe ser definida fundamentalmente para suplir la distribución. A medida que pasa el tiempo y se equilibran los compartimentos de alto flujo y tejidos profundos, va tomando predominancia la eliminación, siendo ésta última exclusiva a partir desde las 5 vidas medias de eliminación de una droga.
Antes de la incorporación de la informática a las infusoras electrónicas, la complejidad de ajustar mentalmente por el anestesiólogo todas las covariables a una velocidad de infusión cambiante en el tiempo, fue un factor limitante del desarrollo de la TIVA. Más aún cuando la dinámica quirúrgica obliga a cambiar el plano adecuado y se vuelve a perder la referencia del momento de la fase distributiva en la que se encuentra. La aparición de los TCI inicia una nueva etapa en la facilitación de la perfusión ajustada a covariables.
La esencia de un sistema TCI es convertir un objetivo de concentración plasmática en una infusión de velocidad variable que se ajusta en el tiempo de la forma como el modelo FC describe la transferencia por distribución a tejidos profundos y la eliminación. La velocidad de perfusión es influida por los parámetros de los modelos, en especial los dos parámetros más importantes que son el volumen central (V1) y el aclaramiento desde V1 (Cl1 = V1 x k10). A mayor V1 mayor es el bolo inicial y por otro lado, la eliminación es el gran determinante de la perfusión. El V1 define también en parte la transferencia a los tejidos profundos caracterizados como V2 y V3, al influir sobre las constantes de transferencia a V2 (k12 = Cl2/V1) y V3 (k13 = Cl3/V1). Al tener V1 influenciados por peso o edad, se impactará en los otros parámetros del modelo. Es por eso que la definición de estos parámetros son claves en la buena descripción de un modelo.
Los modelos son un proceso de ajuste prueba-error basados en niveles plasmáticos medidos y la matemática que mejor describa el proceso. Por eso para algunos autores la incorporación de covariables específicas en la descripción de uno u otro parámetro puede o no ser significativa. Además sólo recientemente se ha ido avanzando en la metodología de consenso que permita hacer a todos los investigadores el mismo proceso.
Modelos de Propofol y TCI
El modelo que se incorporó a las primeras infusoras TCI de propofol fue concursado entre los de Marsh et al 4 , Dyck y Shafer 5 y Tackley et al 6 y fue evaluado en dos estudios con resultados clínicos muy aceptables (Swinhoe et al 7 – 46 pacientes, MDPE 16,2%; Barvais et al 8 – 21 pacientes, MDPE 21,2%). En especial las fases de inducción y de decaimiento posteriores a la detención de la perfusión resultaron mejor descritas. Un estudio prospectivo posterior en más de 400 pacientes, conformaron la base para recomendar las dianas de trabajo clínico. Logró así superar el proceso de regulación e incorporarse al primer TCI comercial, el Diprifusor®.
El TCI Diprifusor® se expandió en muchos países (con excepción de USA y Canadá) y el sistema se probó como robusto y clínicamente efectivo para pacientes jóvenes. Incluso se utiliza en ancianos realizando un ajuste a la baja en la Cp diana, pero sin una evaluación sistemática en esta población. Un año después del lanzamiento al mercado se le introdujo una constante más: el ke0 de 0,26 min-1, que permitió predecir el retraso entre la Cp y comportamiento del efecto, facilitando la titulación. Este modelo efecto representa un equilibrio a los 4 min posterior a un bolo entre el plasma y el efecto. Este valor fue el resultado de los estudios de Martin White et al 9 presentados como tema libre en el 11º Congreso Mundial de Anestesiología (Sydney, 1996), aunque el control del sitio de efecto no fue considerado en el proceso de regulación inicial y con el tiempo nacieron dudas de si ese valor era adecuado para el modelo de Marsh.
Sólo se mantuvo entonces una forma de administración guiada a plasma y no al efecto. Los conflictos provinieron tanto por el tamaño del bolo de carga en la modalidad conducción (target) al efecto, como de lo que se consideró un tiempo de equilibrio muy lento. Como el modelo de Marsh sólo incluye la covariable de peso en el V1 (0,228 l·kg-1), los bolos de carga podían resultar muy grandes para ciertas poblaciones. Por ejemplo, un paciente independiente de su edad, obeso de 140 kg, recibiría 258 mg y una infusión decreciente para alcanzar una diana de 3 ugml-1 y uno de 70 kg, exactamente la mitad del bolo y la infusión. En este caso el cuestionamiento provino de preguntarse si ¿el peso es la única covariable que condiciona el bolo inicial y la infusión en forma lineal? Eso se resolvería más adelante.
En resumen, este modelo Marsh funciona en una población tipo, pero es cuestionado por no incluir la edad, el género, o la masa magra en sus parámetros. El peso en el V1 exclusivamente se lo ve reduccionista y más aún el modelo sitio efector no fue extraído simultáneamente al modelo cinético y con un equilibrio CpCe algo tardío, hecho en parte causal de un bolo de carga aparentemente excesivo.
El modelo comercial de Diprifusor® condicionó el uso a un control electrónico de una jeringa pre-llenada, que generó, unos años después, al aparecer otros propofol, el estímulo para desarrollar TCI abiertos. Conjuntamente progresa la modelación farmacológica y se publica en 1998 el modelo de Schnider et al 10 ,11 , que se considera más atractivo porque incluye covariables para edad, peso y masa magra, e incluía además un ke0 extraído de un mismo estudio PK/PD integrado8. Aparecen además infusoras como “Base Primea®” de Fresenius Kabi y Cardinal Health con la infusora “Asena PK®” que introducen este nuevo modelo junto al TCI de remifentanil y sufentanil.
El modelo de T. Schnider aparentemente más sólido, fue derivado de 24 adultos, y tiene algunas particularidades: un V1 fijo de 4,27 l. Esto hace que, independiente del peso o la edad, el bolo de carga sea muy similar, porque este bolo es mayormente dependiente de este parámetro. La diferencia entre un paciente de 140 kg y otro de 70 kg de la misma edad sería solamente por el aclaramiento, cerca de 2,5 veces mayor. Aquí el cuestionamiento llegó al preguntarse si es el aclaramiento depende del peso en forma lineal. Y respecto al V1 fijo si es razonable que el bolo de carga en un paciente de 140 kg sea igual al de 70 kg de igual edad.
Un tema adicional en el modelo Schnider es que incluye un ke0 de 0,456 min-1, que en este caso implica que el equilibrio plasma-efecto se produciría en 1,7 min, mucho antes que lo descrito por Marsh y otros autores. El problema de un equilibrio tan precoz es asumir que después de un bolo se ha producido un escaso decaimiento de la concentración por distribución y la Cp se equilibraría con el efecto a concentraciones más altas, implicando que el bolo requerido es menor. Lamentablemente los datos presentados por Schnider en forma muy elegante no se ajustan a la práctica clínica porque la metodología usada no es el escenario clínico. Explicaremos esto más adelante.
Comparando ambos modelos, si bien Marsh (Diprifusor®) no es afectado por la edad en el modelo Schnider sí lo es, porque el V2 y la transferencia a ese compartimento cambian con la edad (Figura 1).
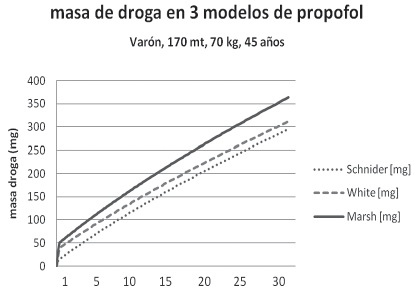
Figura 1 Masa de droga administrada en el tiempo por tres modelos FC de propofol en pacientes tipo.
Para Schnider, entre los 30 y 80 años la disminución del aporte es importante al inicio de la perfusión (aproximadamente 20%), pero pierde relevancia en el tiempo porque después de 1 hora es menos del 10%. Entonces no es claro que el modelo Schnider sea un modelo con adaptación para ancianos, como se pensó en un inicio. El estudio original incluyó 8 pacientes de más de 65 años pero solo uno mayor a 80. Además esta diferencia es mucho menor al 47% de diferencia en la Cp requerida para perder conciencia entre pacientes de 25 y 75 años descrita por varios autores 11 .
Recientemente Martin White presentó un estudio 12 en el cual se agregan covariables de género y edad al volumen de distribución central (V1) y aclaramiento al modelo Marsh, reduciendo el sesgo de 12,6% a 3,2%. Es el llamado modelo White. Este modelo no presentó una constante de equilibrio al efecto.
Evaluación del rendimiento de los modelos
Hasta ahora existen pocas evaluaciones prospectivas de los modelos, y menos aún en poblaciones particulares. Recientemente Glen y Servin 13 estudian 9 pacientes con niveles plasmáticos de sangre arterial y muestra que el modelo de Schnider sería el con menor sesgo. Pero al analizar por fases, se observa que Schnider sobrestima las Cp en la inducción y las subestima en la fase de decaimiento, lo que explica su mejor rendimiento global. Durante el mantenimiento todos los modelos son similares.
En poblaciones particulares los obesos y ancianos se comentan más adelante.
Las implicancias de las diferencias entre los modelos en el aporte de Propofol
El modelo Marsh, a cualquier diana propuesta, aporta la misma cantidad de droga en una base de mg/kg, independiente de la edad o peso. Los ancianos se manejan reduciendo la diana y los obesos, o reduciendo la diana o poniendo un peso menor al real. Este peso de corrección ha sido muy debatido. Pero el avance en modelación dice que sería deseable para reducir la variabilidad poblacional, agregar más covariables a los modelos. Junto a eso las ventajas que aporta el control del sitio de efecto, hacen deseable optimizar el parámetro ke0. El control del modo efecto no es posible con Diprifusor®.
-
Los Obesos
Los modelos también incorporan otras variables que pretendían mejorar su descripción, por ejemplo, la masa magra como covariable de impacto en el modelo de Schnider de propofol y Minto de Remifentanil en las infusoras. Estos usan la ecuación de James14 para masa magra incorporada en algún parámetro (Cl1 en el modelo Schnider). El problema que aparece al usar masa magra como covariable fue la ecuación de masa magra misma, que decrece como valor en los hiper obesos. Esta ecuación funcionaba aceptablemente sólo hasta índices de masa corporal (BMI) > 42 kg/m2 en varones y > 35 kg/m2 en mujeres, y hubo que bloquear las infusoras para el uso en TCI en masas mayores.
Ecuación 1
Varones: 1,10 x Peso (kg)-128x[Peso(kg)2/Altura(cm)2]
Damas: 1,07 x Peso (kg)-148x[Peso(kg)2/Altura(cm)2]
Aún no existe consenso cual sería la ecuación a utilizar para el cálculo de masa magra. Como las ecuaciones de Janmahastian 15 o de Hume 16 .
En los obesos se intentó inicialmente corregir el modelo de Marsh en base a un peso de ajuste 17 ,18 (peso a usar: peso ideal + 0,4 (peso real-ideal)), pero éste mostró ser incluso más inexacto que usar el peso real. En el modelo de Schnider es aún peor el problema, porque tiene dos graves inconvenientes en esta población. Primero el V1 fijo es un mal descriptor del obeso, que tiene un débito cardiaco alto (aunque menor en términos relativos) lo que representa una expansión del V1 y requeriría mayor masa de droga de inducción para superar esta fase la mezcla. Segundo, Schnider describe que la eliminación es influenciada por el peso, la altura y la masa magra, sin influencia de la edad (Ecuación 2).
Ecuación 2
K10 = 0,443 + 0,0107 x (peso-77) – 0,0159 x (LBM-59) + 0,0062 x (altura-177)
Para el caso de los obesos, el problema nace en que si la ecuación de masa magra está mal formulada y describe a los hiper obesos como con menor índice de masa, el valor del aclaramiento total es mayor. Este hecho hace que el modelo de Schnider entregue exceso de droga a estos pacientes 43 .
Con las características de los V1 descritos por los modelos y la influencia de la masa magra en el aclaramiento, con el modelo Schnider un paciente obeso recibe menos propofol en la carga proporcionalmente al peso y un paciente con bajo peso recibe inicialmente 30% menos que con Marsh, pero luego de 30 min Schnider aporta 15% más que Marsh.
Recientemente Cortínez y cols 19 , evaluaron los modelos publicados, encontrando un error absoluto del modelo Schnider de un 42% y en el de Marsh de un 41%, con sesgos positivos (subpredicción) en Schnider y negativos (sobrepredicción) en Marsh.
Con estos datos, este grupo construyó un modelo integrado con los 26 pacientes mesomórficos originales de Schnider y 28 obesos, con los que describen que los volúmenes de distribución son dependientes del peso total pero los aclaramientos deben ser corregidos alométricamente a una potencia de 0,75. Esta relación significa que la función de aclaramiento no crece linealmente con el tamaño corporal del obeso. Es decir, no existe “un” peso a utilizar sino varios en el transcurso de la anestesia 20 .
En la Figura 2 se observa la diferencia de droga administrada por los diferentes modelos a un mismo objetivo de Cp. Schnider sobredosifica más que Marsh usando peso real en relación al modelo Cortínez construido con pacientes obesos.
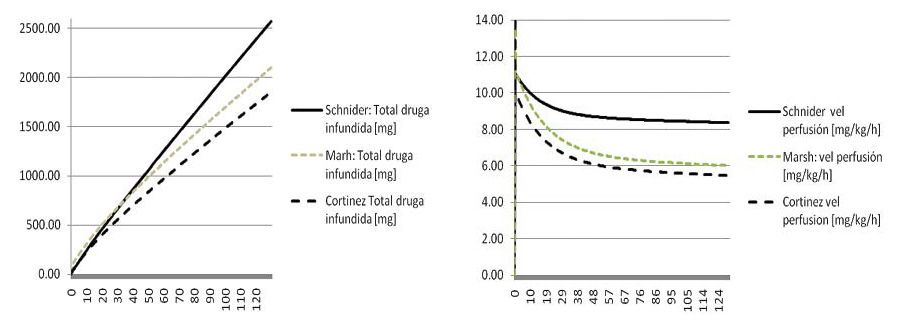
Figura 2 Izq: Masa de droga aportada para mantener Cp 3 µg/ml por el modelo Schnider, Marsh y Cortínez en una paciente mujer de 155 cm, 135 kg de peso, 34 años. Derecha: velocidad de infusión en mg/kg/h para mantener Cp 3 µg/ml.
-
Los Ancianos
En la población mayor de 65 años los datos disponibles son más dispersos y escasos aún, y en los modelos incorporados en los llamados TCI (target controlled infusion) los datos originados de pacientes mayores son mínimos.
Como se dijo, el primer modelo comercial de propofol incluido en el TCI Diprifusor fue el modelo de Marsh, que en sus parámetros no considera la edad. Es decir, tanto los Vd como los Cl son iguales entre jóvenes y ancianos del mismo peso, aportando la misma masa de droga a ambos grupos. Para dar anestesia con este modelo en pacientes ancianos la corrección que se debe hacer es reducir la diana de trabajo asumiendo que las EC50 (sensibilidad) para propofol es menor y que los cambios farmacocinéticos tienen el mismo sentido en todas las fases anestésicas, concepción que los últimos datos rechazan.
Otros modelos (Schnider y White) incluyen edad entre sus covariables, pero no hay estudios prospectivos de validación. El modelo Schnider aporta inicialmente más droga a un joven que a un anciano de igual peso pero después de una hora esta diferencia no crece más. El modelo White no diferencia al inicio pero más tardíamente aumenta un poco la diferenciación entre joven y anciano.
El modelo de Schnider tiene un V1 tanto para jóvenes o ancianos, donde tampoco impacta el peso. Entonces la masa para llenar el V1 es la misma en todo tipo de población y peso. White en cambio, sí diferencia edad y peso en el V1, diferenciando algo más el primer bolo (Figura 3).
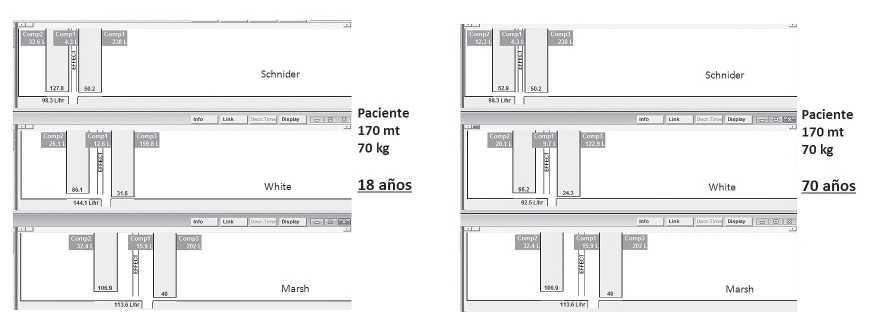
Figura 3 Diferencias en Vd, velocidad de transferencia y eliminación en modelos de Schnider, White y Marsh (de arriba a abajo) en un paciente 70 años (derecha) vs 18 años (izquierda) ambos 170 mt, 70 kg.
Schnider cambia fundamentalmente en transferencia a V2 y tamaño de V2.
White cambia en todos los parámetros y Marsh en ninguno. Simulación TIVA trainer.
White describe que los ancianos tienen menor transferencia a V2, menor V3 y menor eliminación, mientras Schnider sólo describe un menor V2 y menor transferencia a V2.
A pesar de esas diferencias las masas de droga en el tiempo no son muy distintas y se hace evidente que ningún modelo cinético diferencia a esta población específica, como se ve en la Figura 4.
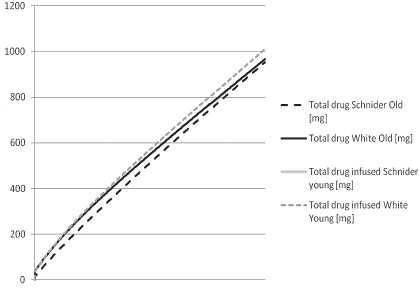
Figura 4 Masa de droga administrada en el tiempo en jóvenes vs ancianos para los modelos White y Schnider en 2 horas de perfusión TCI diana 3 µg/ml. Simulado con Anestfusor® U de Chile.
Aún faltan estudios para confirmar cuál de estos modelos es más recomendable para el uso clínico, y ninguno cumple cabalmente la intuición de que los ancianos requieren menos droga en el tiempo y tienen mayor sensibilidad, o sea requieren Ce menores.
Para aclarar estas dudas estudiamos a pacientes ancianos, entre 69 y 100 años, encontrando que la predicción de los modelos es pobre 21 . El modelo de Marsh (Diprifusor) presenta errores absolutos de 60%; Schnider, originalmente recomendado para ancianos, tiene una subpredicción de más de 40%, es decir, las concentraciones calculadas son mucho más bajas que las reales y el paciente está mucho más profundamente anestesiado de lo que se creía. El modelo de White es sólo levemente mejor, pero siempre fuera del rango aceptado. Con estos datos se deberá ahora ajustar un modelo para ancianos.
Respecto a los menores requerimientos de droga, se estima hasta ahora que es principalmente por razones farmacodinámicas, pero podría ser que gran parte del menor requerimiento en ancianos sanos sea por una mala descripción de la farmacocinética 21 .
Nuestros datos recientes estarían confirmando que los ancianos presentarían tiempos de instalación del efecto más lento y un ke0 con impacto de la edad describe mejor el curso temporal a diferentes edades (Figura 5). Este fenómeno aún no ha sido incluido en los TCI de propofol comerciales. El modelo de Schnider, que a pesar de incorporar un modelo de sitio efector con un nexo dado por un ke0 fijo independiente de la edad, produce como efecto de la transferencia a V2, un tiempo de efecto máximo (TTPE) 15 segundos mayor al TTPE 1,7 min de un paciente joven, pero no suficiente para representar el mayor retraso en manifestarse el efecto en los ancianos.
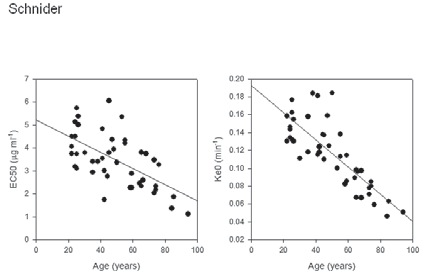
Figura 5 El EC50 y ke0 según edad para el modelo de Schnider. La línea solida representa la regresión lineal basada en las predicciones individuales 21 .
En un estudio de nuestro grupo 21 , que se ve en la Tabla 2, se observa que según el modelo usado, las masas de drogas para alcanzar los respectivos EC50 se diferencian mucho entre los jóvenes y ancianos con el modelo Schnider, pero menos con el modelo White. Esto se explica porque White incluye correcciones en el V1 de edad y peso y Schnider no. Entonces, la menor variabilidad farmacodinámica observada en White sería consecuencia de esta corrección de la cinética y la mayor masa de droga proporcional al EC50 recibida por los ancianos, sería consecuencia de la compensación del decaimiento por distribución producto del enlentecido tiempo de equilibrio.
Tabla 1 Error global (MDAPE) y sesgo (MDPE) tendencia del error global y por fases en modelos Marsh (Diprifusor), White y Schnider
|
MDPE % |
MDAPE% |
MDPE% 1-5 min infusión rápida |
MDPE% Mantención |
MDPE% Recuperación |
|
| Diprifusor |
2,3 (-31-33) |
24,6 (11-37) |
17,7 (-41-71) |
12,7 (-28-53) |
-10,5 (-46-64) |
| White |
-12,6 (32-16) |
21,4(13-37) |
-14,9 (-53-27) |
3 (-29-42) |
-8,7 (-46-64) |
| Schnider |
-0,1 (21-33) |
23,6 (13-42) |
-36,8 (-59-5.7) |
9,9 (-15-63) |
15,5 (-28-96) |
Tabla 2 Ejemplos: masa de droga en bolo para alcanzar el EC50 en pacientes de diferentes edades y 70 kg de peso con ke0 ajustado por edad
|
Modelo Schnider |
Modelo White |
|||||
| Edad |
EC50 |
mg/70 kg |
Ke0 min-1 |
EC50 |
mg/70 kg |
Ke0 min-1 |
| 18 |
4,56 |
178 |
0,16 |
4,7 |
145 |
0,354 |
| 40 |
3,65 |
156 |
0,126 |
4,09 |
140 |
0,282 |
| 60 |
2,83 |
138 |
0,095 |
3,53 |
138 |
0,218 |
| 80 |
2,0 |
122 |
0,063 |
2,97 |
141 |
0,153 |
La respuesta más definitiva se tendrá con un refinamiento del modelo específico para estas edades, donde la corrección FC nos redefinirá si la mayor sensibilidad a propofol es un hecho o sólo un espejismo oculto en la deficitaria descripción FC. Un modelo FC/FD para ancianos en TCI debe representar algunas orientaciones con sentido fisiológico: a) eventualmente para la definición del V1 usar masa magra, que se asocia mejor a la contracción de V1 por la edad; b) para describir los Vd profundos es probable que el peso real sea útil; c) la eliminación tendría relación a la edad; d) un ke0 ajustado por la edad, que refleje la instalación más tardía del efecto; y e) luego podremos conocer los valores de EC50 por edad.
-
Los Niños
En niños el proceso de describir la cinética de propofol ha sido también complejo y lento. Los dos grandes modelos que se disputan la descripción son los de Kataria 22 y Absalon 23 (Paedfusor). Ambos también tienen escasos estudios de validación prospectiva y son limitados a edades de los 3 a 12 años. Estos modelos describen el mayor consumo por distribución y aclaramiento que tienen los niños en relación al adulto.
En niños pequeños, entre 2 meses y 3 años, Sepúlveda y cols, estudian 41 niños con muestras arteriales y confirma que ambos modelos son aceptables en la generalidad pero tienen errores no aceptables en fases específicas y críticas como la inducción y decaimiento, lo que implicaría rediseñar estos modelos para niños pequeños 35 . Para los niños menores de un año la eliminación debería ajustarse al proceso de maduración hepática. En estos pacientes, al igual que los obesos, el ajuste alométrico se considera adecuado para describir la relación del tamaño con la función hepática 36 ,37 .
El modelo efector en niños también ha sido difícil de diseñar. Muñoz y col 24 , describen que para el modelo de Kataria y Paedfusor los tiempos de equilibrio post bolo son más rápidos en niños que en adultos. El otro detalle descrito 25 es que a medida que los niños crecen el tiempo de equilibrio se enlentece (o dicho de otra forma el ke0 se hace más pequeño), asociado a un EC50-95 progresivamente menor.
Prontamente estos datos serán analizados en conjunto y presentados a la comunidad anestesiológica.
Metodología para determinar el ke0 y el sitio efector
Como la droga no actúa en la sangre es necesario describir el retraso en la aparición del efecto y su intensidad. Esto se hace con los modelos FD. En anestesia intravenosa, los modelos FD son descritos como modelos sigmoidales directos, es decir, el aumento de la Cp no es lineal a la aparición del efecto y es el efecto directo sobre el receptor celular el que desencadena el efecto. Ambas descripciones son simplificaciones de la realidad. Es probable que los efectos sean solo parcialmente directos y/o indirectos actuando sobre sistemas neurológicos lejanos, y que la descrita curva concentración-efecto no represente exactamente el sentido del efecto ni la fisiología del proceso (sentido dormido a despierto puede ser por un mecanismo distinto que despierto a dormido). De todas formas las descripciones matemáticas del comportamiento del efecto se han visto útiles en el trabajo clínico, aún sin necesariamente representar la fisiología del proceso.
Se ha discutido mucho de las metodologías e instrumentos usados para evaluar el efecto o su representación matemática, denominada constante de transferencia al efecto (ke0). El retraso en el procesamiento de la respuesta de los EEG, la necesidad de hacer estudios FCFD simultáneos con medición de niveles plasmáticos, si la velocidad de perfusión impacta o no en el valor del ke0 o en la farmacodinamia de la droga, o si el ke0 es impactado por la edad, son temas en discusión. Además existen otras definiciones complejas en torno a qué objetivo clínico representa la condición anestésica. Por ejemplo, J. Mourisse presentó recientemente 26 ,27 información que indicaba que efectos observados de estructuras medidas en la corteza o sub corteza tienen diferentes k e0 (ej. pérdida de reflejo palpebral o inmovilidad) y que tienen distinta pendiente en la representación asociada a BIS.
Por ahora la técnicas paramétricas o no paramétricas se han usado para representar la histéresis o retraso como proceso de primer orden en condiciones de no equilibrio produciendo resultados diferentes si el estudio se hace en bolos mayores a 1.200 ml·h-1 o menores a esa velocidad. Por ejemplo, post bolo manual, el concepto tiempo de efecto máximo (TTPE) 28 ,29,30 es un concepto cinético independiente, pero ha sido cuestionado porque dependería en exceso de la velocidad de administración 31 . Si bien este concepto es interesante porque al ser cinético independiente permitiría al evaluar el TTPE para una droga y calcular el ke0 correspondiente para cada modelo cinético, esto no ha podido ser demostrado en el caso de los hipnóticos, entre otras cosas por dificultades en definir que indicador EEG sería el más adecuado, si el tamaño del bolo influye o no (bolos muy grandes aunque submáximos pueden alterar la hemodinamia y desde allí la cinética), y la velocidad de administración (manual vs infusora), o incluso a errores de definición de la cinética del bolo (ej. tiempo 0 es Cp máxima).
Las diferencias de representación del efecto en los modelos de propofol son en gran parte consecuencia de las diferencias en el tamaño de V1 descrito por estos. El modelo Marsh con un V1 de 15 l en un adulto tipo vs los 4,5 l de Schnider muestra una diferencia de 3 veces, por lo que, el bolo para llenar ese V1 es muy diferente y por lo tanto, el efecto resultante. Como se explicó arriba, el modelo Marsh original, con un V1 muy grande fue sólo pensado para hacer TCI plasma y fue modificado por Struys para ser usado en modalidad sitio efecto en la infusora Primea Orchestra 32 . Struys concluye que el tiempo pico de equilibrio que calculó Schnider de 1,7 min era adecuado, con lo que resultan bolos de inducción más pequeños.
A poco andar se observó que la descripción del efecto de estos modelos era confusa. Las Ce descritas para pérdida de conciencia que pretendían proyectar la mantención y el despertar no cumplían ese objetivo. Por ejemplo, en un estudio del autor usando infusiones a la velocidad de un TCI modo sitio efector (1.200 ml·h-1), el valor de la Ce calculada a la pérdida de conciencia (BIS 70) fue sobre 4,5 µg·ml-1 para Schnider y Marsh modificado por Struys (TTPE 1,7 min), estos valores son poco representativos de las Cp/Ce de trabajo clínico, por ser muy altos para mantener anestesia o proyectar el despertar 31 . Sucede que ambos modelos ajustados a un mismo TTPE de 1,7 min aportan bolos pequeños y sugieren equilibrios tan rápidos que sobreestiman la Ce al momento del equilibrio.
En este caso el error metodológico se produjo porque el TTPE que calculó Schnider para un bolo manual fue trasladado mecánicamente al TCI que tiene la limitante mecánica de una infusora (velocidad máxima 1.200 ml·h-1). En el mismo estudio de Schnider las Cp predichas por el bolo mostraron tener mal rendimiento predictivo. Además un bolo manual de 2 mg·kg-1 en un paciente de 70 kg puede ponerse en 10 segundos, con una infusora se requerirán 42 segundos al menos, lo que hace trasladar el TTPE. También errores de definición de la farmacocinética, como asumir que la Cp es máxima a tiempo cero, son causa de la deficiente descripción.
De todas formas el modelo Schnider es conceptualmente mejor que Marsh, porque al poner una masa de droga por peso (ej, 1,5 mg·kg-1) la Cp será diferente para cada peso, y además por edad. En el caso de Marsh la Cp alcanzada será la misma aun en pesos diferentes (para igual masa de droga por peso) y edades diferentes.
Schnider con su descripción de la cinética (V1 fijo, V2 cambia por edad) produce un pequeño impacto en el TTPE, que se manifiesta más marcadamente en pacientes de más edad. Entonces si bien Schnider describe un ke0 fijo, el TTPE es variable, aunque de poca monta. Lamentablemente este concepto, que es razonable, se diluye por la descripción de un TTPE muy breve.
El nuevo modelo White (Marsh modificado), con aún pocos estudios clínicos, tiene un V1 menor que Marsh, ajustado además a la edad del paciente y por ello aporta menos droga en la inducción. En el tiempo se parece mucho a Schnider, con la salvedad que aporta algo menos droga a los pacientes ancianos después de una hora de infusión. Este modelo tampoco tiene validación prospectiva y originalmente no tiene ke0. Solo recientemente se ha propuesto un valor que difiere bastante del original de Marsh (alrededor de 0,44 min -1) con un ke0 variable con el transcurso de la edad 39 .
En nuestra visión el “problema sitio de efecto” y su representación matemática ke0, ha sido complejo de definir en muchos aspectos. Por ejemplo, es razonable preguntarnos qué tan creíble son los monitores usados, o si el proceso de inducción es de farmacodinamia directa o indirecta (se activan secundariamente otras áreas cerebrales), si el ke0 es o no dependiente de la velocidad de infusión, si cambia con la edad o con el flujo cerebral, etc. Por ahora aparentemente el ke0 sería significativamente impactado por velocidades superiores a 1.200 ml·h-1 pero no a velocidades de trabajo habitual 33 y el ke0 sería dependiente de edad 34 tal como sucede con los niños y otras drogas 40 ,41,42 .
En los modelos hoy disponibles no hay un ke0 ajustados por edad. El modelo sitio efector sería aparentemente más adecuado para la predicción de la mantención y el despertar de los pacientes 34 . La descrita mayor sensibilidad (menor EC50) en pacientes ancianos debe ser reevaluada en su magnitud, ajustando primero los modelos cinéticos mejor a la población geriátrica. Allí conoceremos también mejor la magnitud de la diferencia FD.
Como buen ejemplo de complejidad, en la Tabla 2 se observan los valores propuestos en nuestro estudio, que muestran un ke0 y EC50 variable con la edad para el modelo Schnider, como también la masa de droga a inyectar para alcanzar el EC50 por edad. Dado el efecto de un ke0 variable se produce un tiempo de equilibrio más tardío en el anciano, provocando que el EC50 de la edad correspondiente no tenga una disminución lineal en la masa de droga aportada. Como en nuestro estudio también mostramos que en ancianos el error predictivo de estos modelos es alto (sobre 30% de error absoluto), es esperable que la modelación del efecto también cambie.
Recomendaciones prácticas
Este proceso evolutivo de la descripción de los modelos ha generado confusión en los anestesiólogos prácticos no especialistas en farmacología avanzada.
Mientras se terminan de optimizar los modelos, es recomendable tener algunas recomendaciones para enfrentar la confusión.
Por ejemplo:
-
Es claro que a medida que progresa la perfusión hay menos discrepancia en la descripción entre los modelos, porque el aclaramiento es el parámetro más fácil de extraer y que tiene más relación a la fisiología. Esto es válido para los pacientes sanos con los cuales se estudiaron los modelos, pero aún no tan claro en poblaciones particulares.
-
En pacientes fuera de los modelos (ancianos, pacientes inestables, obesos), es recomendable usar inducciones escalonadas para titular el efecto. Si bien el error de la Cp predicha será mayor, podemos usar la Cp para el efecto clínico como valor tendencial. En obesos es mejor, aunque no óptimo, el modelo Marsh a peso real que Schnider. En ancianos sería White levemente mejor. El modelo Cortinez-Sepúlveda debiera comportarse mejor en jóvenes y obesos por provenir de esa población específica, aunque falta validación prospectiva. La evaluación recientemente presentada muestra una mejoría importante en la inducción y el decaimiento, pero el mantenimiento tiene todavía una subpredicción importante 38 .
-
Es recomendable, siempre que se pueda, hacer inducciones lentas (escalones pequeños 1 µg·ml-1 a 1,5 a 2 µg·ml-1) hasta que el paciente pierda conciencia. Una vez dormido iniciamos el opioide y eventualmente el bloqueo neuromuscular. La Ce de referencia a la pérdida de conciencia es en esta forma de inducción más cercana a la plasmática, al haber menor disociación cinético-dinámica y más representativa de la Ce de mantenimiento. Ningún modelo sitio efector de las infusoras comerciales es plenamente satisfactorio para hacer inducciones al efecto. Schnider sobreestima (pone muy poca droga) y Marsh sobreestima el valor de la Ce 31 .
Tabla 3 Ejemplos: cantidad de droga a aportar con el modelo Schnider para alcanzar la concentración efectiva EC50 a diferentes edades en un paciente de 70 kg con un ke0 ajustado por edad según describe Sepúlveda y cols 34
|
Modelo Schnider |
|||
|
Edad |
EC50 |
mg/70 kg |
Ke0 min-1 |
|
18 |
4,56 |
178 |
0,16 |
|
40 |
3,65 |
156 |
0,126 |
|
60 |
2,83 |
138 |
0,095 |
|
80 |
2,0 |
122 |
0,063 |
¿Qué viene a futuro?
La discusión en torno a los modelos de propofol si bien ha generado confusión en el anestesiólogo práctico ha permitido conocer mucho de los procesos farmacocinéticos. La necesidad de tener que elegir un modelo entre varios, para un paciente individual es un riesgo potencial de error. Es por ello que se inició un proceso de homogenización de los datos con el fin de construir un modelo integrado con la mayor incorporación de covariables. Este proceso está centrado en la iniciativa Open TCI, (www.opentci.org), donde se están recopilando los datos y procesando para el objetivo señalado. Esto facilitará que las infusoras tengan un solo modelo y el anestesiólogo sólo incorpore las variables demográficas correspondientes. El software hará el trabajo de calcular las velocidades de infusión para el tipo de paciente.
Es altamente probable que nunca se obtenga un modelo que incorpore todas las covariables significativas, pero es indudable que un modelo con más datos es mejor predictor, pero para su uso clínico se requiere usarlo asociado a la tecnología de infusión en TCI o sistemas de lazo cerrado en vías de desarrollo.
Incluso así hay déficit en las definiciones y unidades de medida de los conceptos anestésicos. En aviación la definición de velocidad, altura y roce son indiscutidos. En anestesiología la intensidad del proceso nociceptivo o del grado de inconsciencia están lejanos de tener definiciones de magnitud como otros procesos físicos, lo que complejiza mucho nuestras posibilidades de describir los fenómenos con los que interactuamos cada día.
Referencias
- Weaver BM, Staddon GE, Mapleson WW. Tisue/blood and tissue/water partition coefficients for propofol in sheep. Br J Anaesth 2001; 86: 693-703.
- He YL, Ueyama H, Tashiro C, Mashimo T, Yoshiya I. Pulmonary disposition of propofol in surgical patients. Anesthesiology 2000; 93: 986-991.
- Dawidowicz AL, Fornal E, Mardarowicz M, Fijalkowska A. The role of human lungs in the biotransformation of propofol. Anesthesiology 2000; 93: 992-997.
- Marsh B, White M, Morton N, Kenny GN. Pharmacokinetic model driven infusion of propofol in children. Br J Anaesth 1991; 67: 41-48.
- Dyck JB, Shafer SL. Effects of age on propofol pharmacokinetics. Seminars in Anesthesia 1992; 11: 2-4.
- Tackley RM, Lewis GT, Prys-Roberts C, Boaden RW, Dixon J, Harvey JT. Computer controlled infusion of propofol. Br J Anaesth 1989; 62: 46-53.
- Swinhoe CF, Peacock JE, Glen JB, Reilly CS. Evaluation of the predictive performance of a ‘Diprifusor’ TCI system. Anaesthesia 1998; 53 Suppl 1: 61-67.
- Barvais L, Rausin I, Glen JB, Hunter SC, D’Hulster D, Cantraine F, d’Hollander A. Administration of propofol by target-controlled infusion in patients undergoing coronary artery surgery. J Cardiothorac Vasc Anesth 1996; 10: 877-883.
- White M, Engbers FHM, Schenkels MJ, Burm AGL, and Bovill JG. The pharmacodynamics of propofol determined by auditory evoked potientials. Abstract presented in Sydney at the 11th World Congress of Anaesthesiologists A608 (1996).
- Schnider TW, Minto CF, Gambus PL, Andresen C, Goodale DB, Shafer SL, Youngs EJ. The influence of method of administration and covariates on the pharmacokinetics of propofol in adult volunteers. Anesthesiology 1998; 88: 1170-1182.
- Schnider TW, Minto CF, Shafer SL, Gambus PL, Andresen C, Goodale DB, Youngs EJ. The influence of age on propofol pharmacodynamics. Anesthesiology 1999; 90: 1502-1516.
- White M, Kenny GN, Schraag S. Use of target controlled infusion to derive age and gender covariates for propofol clearance. Clin Pharmacokinet 2008; 47: 119-127.
- Glen JB, Servin F. Evaluation of the predictive performance of four pharmacokinetic models for propofol. Br J Anaesth 2009; 102: 626-632.
- James WPT. Research on obesity. London, Her Majesty’s Stationary Office (1976).
- Janmahasatian S, Duffull SB, Ash S, Ward LC, Byrne NM, Green B. Quantification of lean body weight. Clin Pharmacokinet 2005; 44: 1051-1065.
- Hume R. Prediction of lean body mass from height and weight. J Clin Pathol 1966; 19: 389-391.
- Albertin A, Poli D, La Colla L, et al. Predictive performance of ‘Servin’s formula’ during BIS-guided propofol-remifentanil target-controlled infusion in morbidly obese patients. Br J Anaesth 2007; 98: 66-75.
- La Colla L, Albertin A, La Colla G, et al. No adjustment vs adjustment formula as input weight for propofol target-controlled infusion in morbidly obese patients. Eur J Anaesthesiol 2009; 26: 362-369.
- Cortinez LI, Penna A, Olivares L, Sepúlveda P. Propofol pharmacokinetics in obese patients. (Abstract. World SIVA abril 2009).
- Cortínez LI, Anderson BJ, Penna A, Olivares L, Muñoz HR, Holford NHG, Struys MMRF, Sepúlveda P. Influence of obesity on propofol pharmacokinetics: derivation of a pharmacokinetic model. British Journal of Anaesthesia 2010; 105 (4): 448-456.
- Sepúlveda P, Cortinez LI, Vega R, Montalván C. Derivation and Prospective Validation of Four Pharmacokinetic-Pharmacodynamic models in Elderly Patients. Abstract Congreso Chileno de Anestesia. Primer encuentro de europanamericano de farmacología aplicada. Mayo 2011. Rev. Chil. Anest 2011; 40: 128.
- Kataria BK, Ved SA, Nicodemus HF, Hoy GR, Lea D, Dubois MY, Mandema JW, Shafer SL. The pharmacokinetics of propofol in children using three different data analysis approaches. Anesthesiology 1994; 80: 104-122.
- Absalom A, Kenny G: ‘Paedfusor’ pharmacokinetic data set. Br J Anaesth 2005; 95: 110.
- Muñoz HR, Leon PL, Fuentes RS, Echevarria GC, Cortinez LI. Prospective evaluation of the time to peak effect of propofol to target the effect site in children. Acta Anesthesica Scandinava 2009; 53 (7): 883-890.
- Jeleazcov C, Ihmsen H, Schmidt J, Ammon C, Schwilden H, Schüttler J, Fechner J. Pharmacodynamic modelling of the bispectral index response topropofol-based anaesthesia during general surgery in children. British Journal of Anaesthesia 2008; 100 (4): 509-516.
- Mourisse J, Lerou J, Struys M, Zwarts M, Booij L. Multi-level approach to anaesthetic effects produced by sevoflurane or propofol in humans: 1. BIS and blink reflex. Br J Anaesth 2007; 98: 737-745.
- Mourisse J, Lerou J, Struys M, Zwarts M, Booij L. Multi-level approach to anaesthetic effects produced by sevoflurane or propofol in humans: 2. BIS and tetanic stimulus-induced withdrawal reflex. Br J Anaesth 2007; 98: 746-755.
- Minto CF, Schnider TW, Gregg KM, Henthorn TK, Shafer SL. Using the time of maximum effect site concentration to combine pharmacokinetics and pharmacodynamics. Anesthesiology 2003; 99: 324-333.
- Nigrovic V, Amann A. Time to maximum effect site concentration. Anesthesiology 2004, 100: 1319; author reply 1320-1.
- van Meurs WL, Nikkelen E, Good ML. Comments on using the time of maximum effect site concentration to combine pharmacokinetics and pharmacodynamics. Anesthesiology 2004; 100: 1320-1321.
- Sepúlveda PO, CL, Recart A, Muñoz HR. Predictive ability of propofol effect-site concentrations during fast and slow infusion rates. Acta Anaesthesiol Scand 2010; 54: 447-452.
- Struys MRF, DST, Depoorter B, Versichelen LFM, Mortier EP, Dumortier FJE, Shafer SL, Rolly G. Comparison of Plasma Compartment versus Two Methods for Effect Compartment-controlled Target controlled Infusion for Propofol. Anesthesiology 2000; 92: 399-406.
- Doufas AG, BM, Bjorksten AR, Shafer SI, Sessler DI. Induccion speed is not a determinant of propofol pharmacodynamics. Anesthesiology 2004; 101: 1112-1121.
- Sepúlveda PO, Fuentealba A, Cortínez LI. Importance of age as covariable for determining the drug plasma-site effect equilibration time for a TCI propofol pharmacokinetic model. Abstract Eurosiva 2010 Helsinsky.
- Sepúlveda P, Saez C, Penna A, Solari S, Guerra I, Cortínez LI. Performance Evaluation of Paediatric Propofol Pharmacokinetic Models in Children under 3 Years of Age. Congreso Chileno de anestesia 2010 (abstract), Br J Anaesth 2011 (in Press).
- Allegaert K, de Hoon J, Verbesselt R, et al. Maturational pharmacokinetics of single intravenous bolus of propofol. Paediatr Anaesth 2007; 17: 1028-1034.
- Sumpter A, Anderson BJ. Paediatric pharmacology in the first year of life. Curr Opin Anaesthesiol 2009; 22. Epub ahead of print.
- Sepúlveda P, Cortinez LI, Fuentealba A. Evaluación prospectiva del modelo Farmacocinético y Farmacodinámico de propofol en obesos. Abstract Congreso Chileno de Anestesia y Encuentro europanamericano de farmacología aplicada, mayo de 2011. Rev. Chil. Anest 2011; 40: 132.
- Sepúlveda P, Fuentealba A. Estimation of the plasma-effect-site equilibration rate constant (ke0) for the White model of propofol using BIS and IoC with a non-parametric approaches, EuroSiva Milan 2009, Free Abstarct.
- Scott JC, SD, Decreased fentanyl/alfentanil dose requirement with increasing age: a pharmacodynamic basis. J Pharmacol Exp Ther 1987; 240: 159-166.
- Sorooshian SSFS, Michael A. MS, Eastwood N, Boyd A, Hull Ch, Wright P. Pharmacokinetics and pharmacodynamics of cisatracurium in young and elderly adult patients. Anesthesiology 1996; 84: 1083-1091.
- Jeleazcov C, IH, Schmidt J, Ammon C, Schwilden H, Schüttler J. Fechner J. Pharmacodynamic modelling of the bispectral index response to propofol-based anaesthesia during general surgery in children. Br J Anaesth 2008; 100: 509-516.
- Sepúlveda P. Un Problema Gordo. Rev Chil Anest 2008; 37: 113-117.