ANÁLISIS DE PROPORCIONES

Jorge Dagnino S. ¹

---

Rev. chil. anest. Vol. 43 Número 2 pp. 134-138|https://doi.org/10.25237/revchilanestv43n02.12 PDF|ePub|RIS

---

• El análisis de proporciones puede hacerse a través de la estimación o de un test z.

• Más comúnmente, se recurre a la prueba de 2 o, cuando los números son pequeños, el test exacto de Fisher.

• Los errores en el uso y lectura del test de 2 son frecuentes: uso cuando el tamaño de la muestra es pequeño, no realizar la corrección de Yates, análisis post hoc de tablas 2 x n, no tomar en cuenta categorías ordenadas en tablas 2 x n.

• El error más frecuente en el uso del test de Fisher es no considerar las dos colas.

En artículos previos se vio el manejo de los datos medidos en una escala numérica y el uso de las pruebas de hipótesis apropiadas, paramétricas o no paramétricas, y la estimación de un intervalo de confianza. Este capítulo describe las aproximaciones posibles, también como pruebas de hipótesis o estimación, cuando las variables son medidas en una escala nominal.

Los datos categóricos son comunes en la investigación biomédica y por ende en las publicaciones. Se originan cuando los individuos se dividen en uno de dos o más grupos mutuamente excluyentes. En una muestra, el número de individuos que cae en un grupo particular se denomina frecuencia y los datos son presentados en una tabla de frecuencias o tabla de contingencia; la evaluación de estos datos se denomina análisis de frecuencias.

Los métodos de análisis variarán de acuerdo al número de categorías envueltas, si estas están ordenadas o no, del número de grupos independientes de individuos, del tamaño muestral y de la naturaleza de la pregunta planteada. Cuando la variable de interés concierne a un solo grupo, se puede usar una aproximación z a la distribución binomial; cuando son dos o más grupos independientes, se puede usar una extensión del procedimiento anterior, una prueba de 2 o un test exacto de Fisher; cuando son dos grupos relacionados se puede usar el test de McNemar, una modificación de 2.

ESTIMACIÓN

La proporción π de una población con un determinado atributo (vivo o muerto, hipertenso o normotenso) es descrita con la cuenta de los individuos con dicha característica con respecto al total, de tal manera que π = número de casos/n. La proporción con el otro atributo es 1- π; π es también la probabilidad de la presencia de ese atributo en la población. Estas afirmaciones suponen que cada miembro de la población pertenece a una de dos clases y que la proporción de la población perteneciente a una de las clases permanece constante. Estas relaciones pueden resumirse así:

π ₁ + π ₂ = 1 π ₁ = 1 – π ₂

Una proporción es un caso especial de una media donde los éxitos son igual a 1 y los fracasos a cero. Se puede decir así que π juega el mismo rol que µ en una población distribuida normalmente; suponiendo que M miembros de una población de N individuos tienen un determinado atributo, N-M individuos no poseen ese atributo dándose que:

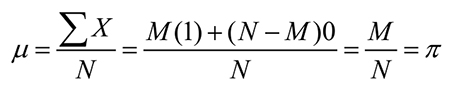
Igualmente, el error estándar de una distribución de medias, de acuerdo con el teorema del límite central, es igual a σ/√N, y la distribución de la proporción tiene una media de π y un error estándar de √ π(1- π)/N. La aproximación z supone que cada miembro de la muestra es seleccionado en forma independiente de todos los otros miembros y es válida cuando Nπ y N(1- π) es > a 5.

Al hacer la estimación de estos parámetros a través de una muestra, se substituye π por p, como la proporción en la muestra; frecuentemente también se designa como p indicando la estimación desde la muestra, de manera análoga a la notación de X y , σ y s. En estas circunstancias el error estándar de la proporción es:

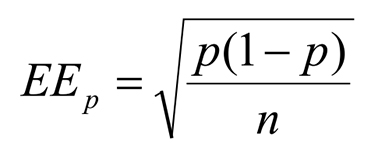
El intervalo de confianza 95 de esta proporción se calcula con p ± 1,96*EEP. La cifra de 1,96 en la distribución normal estándar (z) corresponde al punto que separa el 95% central del 2,5% de cada cola. La cifra correspondiente a 99% y 1% respectivamente es de 2,575, de donde fluye que para calcular el intervalo de confianza 99 se substituye, en la fórmula precedente, el 1,96 por el 2, 575. Por ejemplo: en una muestra de 120 pacientes mayores de 65 años que van a ser operados, 34 son hipertensos:

La proporción de hipertensos es:

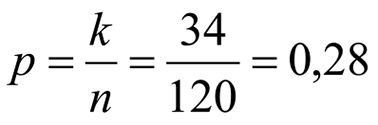
El error estándar de la proporción:

y los límites de confianza LC₉₅ = 0,28 ± 1,96*0,041 = desde 0,20 hasta 0,36. El cálculo subraya la importancia que tiene el tamaño de la muestra en la precisión de una estimación; si se calculan los límites de confianza 95 del mismo ejemplo de arriba pero con un n=10 este intervalo aumenta a 0,006 hasta 0,554 (con un EE_p de 0,14). Esto subraya el concepto que el resultado obtenido de trabajos con pocos casos debe ser tomado con mucha cautela pues la estimación es poco precisa.

Esta aproximación no es válida para muestras pequeñas o cuando p es cercana a cero o uno pues en estas circunstancias el IC queda trunco hacia cero o hacia uno pues no puede sobrepasar estos límites; tanto np como n(1-p) deben ser superiores a cinco.

PRUEBAS DE HIPÓTESIS PARA UNA PROPORCIÓN

La aproximación z puede usarse para una prueba de hipótesis con una sola proporción (p_o, observada), donde esta se compara con otra proporción conocida (p_c), control o teórica. Sigue el mismo raciocinio ya visto donde z = diferencia de proporciones/error estándar, calculado aquí usando la proporción control:

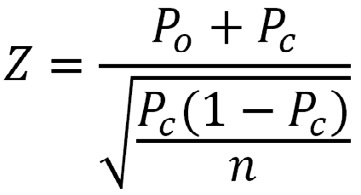
PRUEBAS DE HIPÓTESIS PARA DOS PROPORCIONES

• 1) Test Z:

Para evaluar la diferencia entre dos proporciones independientes, se usa el error estándar de la diferencia calculado con un valor de p mezclado: p=n₁p₁+n₂p₂)/(n₁+n₂).

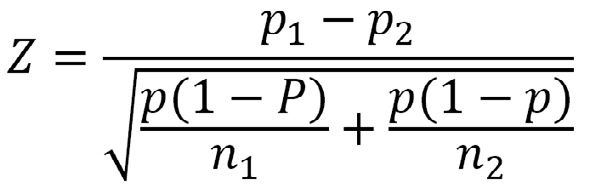
El método, al ser una aproximación discreta a una normal continua, arroja valores de z que son siempre superiores a los que debieran ser, lo que produce un sesgo en el sentido de encontrar un efecto cuando en realidad no existe.

• 2) Tablas de contingencia:

Las tablas de frecuencias presentadas simultáneamente se denominan tablas de contingencia que se emplean para registrar y analizar la relación entre dos o más variables cualitativas. En su forma más simple se denominan de 2 por 2, 2 filas y 2 columnas, donde los datos categóricos son las cuentas que se incluyen en una de dos categorías. La primera extensión es de 2 por c columnas y luego las de f filas por c columnas; puede decirse que en estos casos, con más de dos filas o columnas, la aproximación, como veremos, es análoga a un análisis de varianza. En cualquier caso, es importante destacar que los cálculos deben ser hechos a partir de la cuenta de los individuos o sucesos y no a través de otros datos derivados de esos números como porcentajes, proporciones, promedios u otros.

Las pruebas de hipótesis usadas son el test z o una prueba de 2 para una muestra; cuando son dos muestras relacionadas o pareadas, un test de McNemar; esta situación se da cuando la medición de interés se hace dos veces en los mismos pacientes. Por ejemplo, cuando se comparan dos procedimientos para medir una característica o cuando se comparan las opiniones de dos expertos. Para dos muestras independientes, una prueba de 2 y el test exacto de Fisher, y para más de 2 muestras, el test Q de Cochran o una extensión del 2 o del test de Fisher. En este artículo nos limitaremos a describir el 2 y el test exacto de Fisher por ser los más comunes en la literatura.

• 3) Test de chi cuadrado:

2, la letra griega, se usa para denominar el test y 2, letra del alfabeto español, para el estadístico que se calcula en la prueba. Puede ser usado para evaluar una diferencia o bien una asociación. Al igual que con el resto de las pruebas de hipótesis, el cálculo se basa en que no hay diferencia, en la hipótesis nula. Para explicar el raciocinio, se puede usar la figura estándar de una tabla 2 x 2 donde las celdas a, b, c y d representan las cuentas, A, B, C, D son los totales marginales y N el número total.

	Grupo 1	Grupo 2
Resultado Presente	a	B	C
Resultado Ausente	c	D	D
	A	B	N

El raciocinio se basa en la hipótesis nula de que no hay diferencias entre los grupos. Por lo tanto, se espera que a y b sean cada uno aproximadamente la mitad de C y c y d la mitad de D. Estos son los valores esperados en cada celda. Luego se comparan estos valores con los observados en la realidad. Si la hipótesis nula es verdadera, los valores observados y esperados no diferirán grandemente, pero mientras más difieran es evidente que la probabilidad que la hipótesis nula sea cierta va disminuyendo. La suma de esas diferencias en cada celda, al cuadrado para eliminar el signo y divididas por el valor esperado, es el valor de 2. Este valor se compara con la distribución teórica para cada grado de libertad obteniéndose así el valor de p. Cuando es igual o mayor que el límite que separa el 95% de la distribución del 5% restante se habla de p < 0,05.

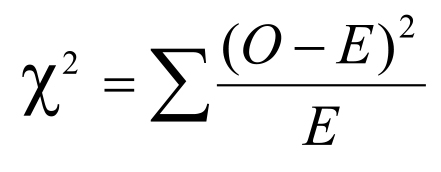
Como todo estadístico, este puede tener un rango de valores determinado por la variabilidad muestral. Este también depende del número de tratamientos que se comparan, expresado en los grados de libertad (ν). En general el cálculo es:

ν = (f – 1)(c – 1)

donde f = número de filas y c = número de columnas en la tabla. Para una tabla de 2 por 2 (2-1) (2-1) = 1 g.l.

Es inapropiado usar un test de 2 cuando el tamaño total de la muestra es < 20 o si este está entre 20 y 40 y el valor esperado más bajo es ≤ 5; también en tablas de contingencia de 2 por k filas, si ≥ 20% de las celdas tienen un valor esperado ≤ 5 o cualquiera < 1. Es importante recalcar que estas cifras se refieren a los valores esperados y no a los números obtenidos. La razón es aparente al observar la fórmula donde un valor esperado muy bajo en el denominador aumenta desproporcionadamente el valor final de 2.

En una tabla de 2 x 2, cuando el tamaño de la muestra es pequeño (≤ 100) o una de las celdas tiene un n observado ≤ 10, se debe usar la corrección de Yates, o corrección de continuidad, cuyo efecto es disminuir levemente el valor de 2:

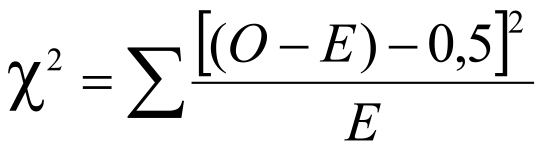
La razón de esta corrección reside en que, al igual que con el caso de z, la distribución de los valores de 2 es discreta mientras que la distribución teórica de 2 es continua.

Cuando los números son bajos, se debe usar un test exacto de Fisher. Alternativamente, pueden colapsarse celdas teniendo cuidado que dicha maniobra tenga sentido biológico y que haya sido contemplada a priori y no post hoc, al revisar los resultados. Por el otro lado, cuando hay dos grupos en escala numérica y se usa la tabla reduciendo su información a una nominal se puede producir un error tipo II, esto es, aceptar la hipótesis nula cuando en realidad debió haberse rechazado. Por ejemplo, al analizar la frecuencia de una complicación (presencia o ausencia) en relación a la edad, se simplifica a una dicotomía de, por ejemplo, > 49 años y < de 50 años, en vez de analizarla en su continuo con un test t comparando la edad promedio en los dos grupos.

En tablas de contingencia con tres o más resultados, un resultado significativo de un valor de 2 elevado no nos dice cuales pares o grupos de resultados son los responsables del efecto. El resultado es análogo al de un análisis de varianza y por cada comparación directa entre pares debe hacerse un ajuste de Bonferroni.

Se puede resumir el mal uso de 2 o en los siguientes puntos:

• Uso de porcentaje o proporciones en el cálculo de 2.

• n pequeños (no usar):

  • n total < 20

  • más del 20% de las celdas con n esperado ≤ 5

• No usar corrección de Yates (n total < 100 o cualquier celda ≤ 10)

• Análisis post hoc tablas 2 x n

• No tomar en cuenta categorías ordenadas en tablas 2 x n

• 4) Test exacto de Fisher:

Cuando es inapropiado usar un 2, la alternativa es el test exacto de Fisher. La razón de no usarlo de preferencia es porque los cálculos pueden hacerse engorrosos con un n grande. Sin embargo, la disponibilidad de computadores más potentes ha hecho factible su cálculo con igual facilidad, aunque no todos los programas lo incluyen. El test calcula la probabilidad exacta de observar la distribución obtenida o cualquiera más extrema. A diferencia del 2, el test puede calcularse con una o dos colas. Como en la mayoría de los casos corresponde el cálculo con dos colas, es un error frecuente en la literatura su cálculo con una cola, error que se aumenta pues frecuentemente ni siquiera se menciona el tipo de cálculo efectuado.

El cálculo se hace con la fórmula:

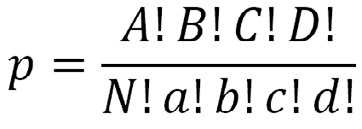
El cálculo se hace para las distribuciones posibles de una tabla de contingencia y se suman las probabilidades de observar una distribución como la encontrada o cualquiera más extrema que esa, hacia una de las colas o incluyendo las dos colas. La manera de hacer los cálculos y la importancia de hacer un test de dos colas puede verse con el siguiente ejemplo: en 28 pacientes con morfina peridural, 1 ó 3 mg, se compara la incidencia de prurito donde 1 de 12 que recibieron 1 mg, y 7 de 16 pacientes que recibieron 3 mg presentaron prurito. Se hace el cálculo de p correspondiente a esta resultado arrojando una p = 0,041:

 

	CON	SIN		p=8!20!2!6!28!1!11!7!9!
MORFINA 1 mg	1	11	12
MORFINA 3 mg	7	9	16
	8	20	28

Se calcula después la p correspondiente a la distribución más extrema que esta, conservando los totales marginales, lo que da una probabilidad de 0,0041.

 

	CON	SIN		p = 0,0041
MORFINA 1 mg	0	12	12
MORFINA 3 mg	8	8	16
	8	20	28

La suma de ambas es igual a 0,0481 lo que resulta estadísticamente significativa con α=0,05. Esto corresponde a un test de 1 cola. Para observar la otra cola, se grafican las otras distribuciones posibles conservando los totales marginales y se calcula p para cada una de ellas:

 

	CON	SIN		p = 0,0170
MORFINA 1 mg	2	10	12
MORFINA 3 mg	6	10	16
	8	20	28

 

	CON	SIN		p = 0,0309
MORFINA 1 mg	3	9	12
MORFINA 3 mg	5	11	16
	8	20	28

 

	CON	SIN		p = 0,0289
MORFINA 1 mg	4	8	12
MORFINA 3 mg	4	12	16
	8	20	28

 

	CON	SIN		p = 0,0143
MORFINA 1 mg	5	7	12
MORFINA 3 mg	3	13	16
	8	20	28

 

	CON	SIN		p = 0,0357
MORFINA 1 mg	6	6	12
MORFINA 3 mg	2	14	16
	8	20	28

 

	CON	SIN		p = 0,0040
MORFINA 1 mg	7	5	12
MORFINA 3 mg	1	15	16
	8	20	28

 

	CON	SIN		p = 0,00016
MORFINA 1 mg	8	4	12
MORFINA 3 mg	0	16	16
	8	20	28

 

Se puede ver que existen otras tres distribuciones más extremas que la observada pues tienen menor probabilidad. La suma de estas tres a las dos primeras da una p total para un test de dos colas de 0,088, no significativa con α = 0,05.

 

Referencias

 

1. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
2. Armitage P, Berry G. Estadística para la investigación médica. 3ªEd, Madrid: Harcourt Brace, 1997.
3. Bland M. An Introduction to Medical Statistics. 3rd Ed., Oxford: OUP, 2006.
4. Dawson-Saunders B, Trapp RG. Bioestadística médica. México D.F: Manual Moderno, 1993.
5. Fleiss JL. Statistical methods for rates and proportions. Wiley & Sons: New York, 1981.
6. Glantz SA. Primer of Biostatistics. New York: McGraw-Hill, 1992.
7. Portney LG, Watkins MP. Foundations of Clinical Research. Applications to practice. 2nd ed. Upper Saddle River: Prentice-Hall, 2000.
8. Zelterman D, Louis T. Contingency tables in medical studies. En Bailar III JC, Mosteller F. Medical uses of statistics. Boston: NEJM Books, 1992.