INTERVALOS DE CONFIANZA

Jorge Dagnino S. ¹

Rev. chil. anest. Vol. 43 Número 2 pp. 129-133|https://doi.org/10.25237/revchilanestv43n02.11 PDF|ePub|RIS

• Los resultados obtenidos a partir de una muestra son aproximaciones a los verdaderos valores de la población. La estimación puede ser puntual, una media por ejemplo, o por intervalo, la media está entre ciertos límites, denominados de confianza. Este expresa la probabilidad de que la media poblacional se encuentre dentro de ese intervalo.

• El ancho del intervalo de confianza permite estimar el grado de imprecisión de la estimación; es inversamente proporcional al tamaño de la muestra.

• La estimación se hace para un determinado nivel de confianza, usualmente 95% o 99%.

• Se pueden calcular intervalos de confianza para medias, varianza y desviación estándar, medianas, proporciones, coeficientes de correlación, líneas de regresión, razones de ventajas (odds ratios), riesgos relativos, las diferencias entre todos los anteriores, y otros.

En otro artículo, se mencionó que en la comparación de muestras hay básicamente dos aproximaciones estadísticas: las pruebas de hipótesis y la estimación, y se hizo una descripción general de aquellas. En esta oportunidad, se desarrollarán algunos conceptos referentes a la estimación y se hará una comparación entre ambos métodos para mostrar que, más que opuestos, son y deben ser complementarios.

ESTIMACIONES E INCERTIDUMBRE

Los resultados obtenidos en un trabajo de investigación son una mera aproximación a aquellos que se habrían observado de haber podido estudiar a todos los individuos con la característica que nos interesa. Las estimaciones hechas a partir de esos resultados pueden ser puntuales o bien de intervalo. Aquellas, calculando variables tales como la media, la desviación estándar u otras, las que, si bien constituyen la mejor estimación que podemos hacer del verdadero valor poblacional, no dan idea alguna de la imprecisión que tiene esa estimación. La estimación por intervalos permite conocer el rango de valores en que podemos confiar que está el verdadero valor poblacional; por lo tanto, permite dimensionar la imprecisión de la estimación puntual y este es su principal propósito. Se puede decir que la estimación puntual constituye el centro de la estimación, que el intervalo dimensiona los radios de ella y que su ancho es una medida de la imprecisión envuelta.

La estimación por intervalo se hace para un determinado grado de confianza. Este indica la probabilidad que el intervalo contenga en su interior al parámetro en cuestión. Para la mayoría de las estimaciones por intervalos – como es el caso de medias, desviaciones estándar, proporciones como riesgo relativo o razón de ventajas (odds ratio), coeficientes de regresión – se puede asumir que la distribución de los valores de interés sigue una distribución Normal y lo mismo vale para las diferencias entre ellos. El cálculo del grado de confianza sigue el raciocinio presentado sobre el área bajo una curva Normal en un artículo anterior; por el mismo motivo, existe una relación cercana entre los intervalos de confianza y las pruebas de hipótesis de dos colas como veremos luego.

INTERVALO DE CONFIANZA DE LA MEDIA

Al afirmar que la media aritmética del IMC en una muestra de varones entre 20 y 65 años es de 28 kg·m-2 se está haciendo una estimación puntual de µ, la media poblacional (la de los varones entre 20 y 65 años); es la mejor estimación pero no da una idea de la precisión de dicha estimación. En cambio, al afirmar que el promedio del IMC en la muestra mencionada es algún número entre 26,3 y 29,7 kg·m-2 se está haciendo una estimación de intervalo que sí dimensiona la imprecisión de la estimación puntual.

El teorema del límite central muestra que el error estándar de la media (ESM) es una estimación de la precisión con que la media muestral representa a la media poblacional. Multiplicando el error estándar por un factor permite calcular, sumando y restando desde el valor de la media, el área bajo la curva de la distribución normal estándar. Por ejemplo, media ± 3 ESM es un intervalo de confianza (IC) del 99,7% pues la probabilidad de obtener un valor de una distribución normal estándar más allá de 3 desviaciones estándar es de 0,3%. El factor para dejar comprendido en el intervalo el 95% del área bajo la curva es de 1,96 ESM pues el intervalo de valores comprendidos entre:

y

comprende el 95% del área bajo la curva normal estándar.

Como raramente se conoce el error estándar poblacional que requiere para su cálculo conocer la varianza poblacional (σ), se usa la varianza muestral para calcular una estimación del error estándar como puede verse en la fórmula ya conocida:

Estimación del error estándar:

Es evidente que mientras más pequeño es el tamaño de la muestra, mayor es la imprecisión de la estimación pues el intervalo aumenta. Además, con n < 100 debe usarse la distribución de t ajustada para el tamaño de la muestra (los grados de libertad); el efecto es aumentar el factor desde ese 1,96 a 2 o más si n ≤ 60; con ello aumenta el intervalo calculado.

Los intervalos de confianza de análisis no paramétricos, como por ejemplo de medianas y otros cuartiles, también pueden ser calculados, aunque sólo con un nivel aproximado de confianza.

Un intervalo de confianza es más impreciso mientras más ancho resulte. Esto depende esencialmente de tres factores:

• El tamaño de la muestra: muestras más grandes darán resultados más precisos y por ende intervalos de confianza más angostos. El corolario es que hay que desconfiar de las estimaciones provenientes de muestras pequeñas, afirmación que vale la pena repetir una y otra vez.

• La variabilidad de la característica que se estudia: entre y dentro de la muestra, de errores de medición u otras fuentes.

• El grado de confianza requerido: mientras más confianza se necesita, más ancho es el intervalo (Figura 1).

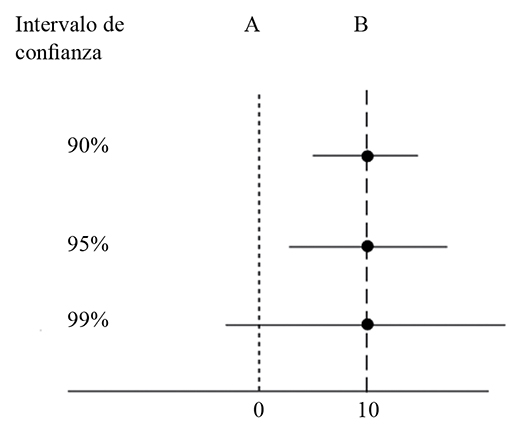
Figura 1 En la Figura aparece la ausencia de diferencia en A (la hipótesis nula) y en B la estimación puntual de la diferencia encontrada. Las barras muestran la amplitud de los intervalos de confianza 90, 95 y 99% y el valor de P inferido del hecho que el intervalo de confianza respectivo incluye o no a la hipótesis nula. Con estos datos se puede estimar que P > 0,01 y < 0,05.

Como ya se dijo, independientemente del ancho del intervalo, la estimación puntual calculada en la muestra es la mejor estimación del valor de ese parámetro en la población.

Ya que la mayor parte de la investigación biomédica envuelve comparación entre grupos, frecuentemente lo que más interesa es analizar la diferencia entre las medias de las muestras o de las proporciones. El raciocinio para determinar los intervalos de confianza de las diferencias es igual al ya presentado. Siguen dos ejemplos ilustrativos:

1. Para evaluar el efecto de una droga sobre la presión arterial, a un grupo se le da la droga en cuestión y a otro un placebo, y luego se comparan las presiones arteriales obtenidas. La media en el grupo con placebo fue de 55 mmHg y la media del grupo con la droga fue de 65 mmHg, para una diferencia de 10 mmHg. El intervalo 95% de confianza (IC₉₅) va de 1 a 19 mmHg y el de 99% de confianza va de -4 a 24 mmHg (Figura 1).

2. La incidencia de náuseas y vómitos en el postoperatorio de pacientes que reciben un antiemético es de 15% comparado con 40% de aquellos con un placebo (n = 100). La diferencia es de 25% y el IC₉₅ de esta diferencia va de 16,1 a 33,9%; el IC₉₉ va de 13,5 a 36,5%.

Con estas cifras de los ejemplos podemos decir que:

• Los valores de 10 mmHg y de 25% son las mejores estimaciones que podemos hacer de las verdaderas diferencias entre los grupos.

• El rango planteado por el intervalo de confianza no excluye que el valor de la verdadera diferencia pueda estar fuera de ese rango pero que es poco probable que así sea.

• Los IC₉₅ muestran la imprecisión de las estimaciones puntuales, algo que solo se podría mejorar con un aumento del tamaño muestral.

• En el primer caso el IC₉₅ no incluye el cero pero si lo hace el IC₉₉: se puede decir entonces que la p asociada es < a 0,05 pero > a 0,01. En el segundo caso, ninguno de los dos IC incluye el cero, la hipótesis nula, por lo que se puede afirmar que la p asociada es < a 0,01.

ESTIMACIONES O PRUEBAS DE HIPÓTESIS

Ha habido una tendencia creciente en la literatura médica a hacer mayor uso de métodos estadísticos y ha aumentado su complejidad y sofisticación. Lamentablemente, con demasiada frecuencia, el análisis de los resultados y la lectura de ellos se limita a obtener un resultado de significativo o no significativo. Los valores de p, que entregan sólo esa parte de la información pero nada sobre la magnitud del efecto, han pasado a ser una especie de fetiche en la literatura médica. Sin embargo, la cuantificación de los resultados mediante estimaciones es absolutamente esencial si se pretende hacer un juicio ponderado de los resultados de una investigación. El uso de un determinado medicamento en clínica debe depender de la magnitud del efecto y de cuan consistente es, y no de si es estadísticamente diferente de un placebo o de otra droga. Además, en último término, siempre debe haber conciencia que los resultados que se obtienen son básicamente inciertos y que es indispensable tener una idea de cuan inciertos son.

Los intervalos de confianza dan esa información no contenida en el valor de p y la entregan en las mismas unidades que el parámetro medido. Muestran la incertidumbre o falta de precisión de la estimación que hemos hecho, dando una idea de lo informativo o confiable del estudio en cuestión. También permiten estimar el rango de la p.

La p, sin embargo, da información que el intervalo de confianza no es capaz de entregar. Una P = 0,0001 da una mejor idea de lo extremo de las probabilidades que el hecho que un valor nulo esté fuera del intervalo 95% de confianza. Dicho esto, el valor de P no debe tomarse como una medida de la fuerza de la evidencia ya que P es la probabilidad de equivocarse al decir que hay un efecto cuando la hipótesis nula es correcta, la probabilidad de ocurrencia de los falsos positivos. En ningún caso es la probabilidad que la hipótesis alternativa, los verdaderos positivos, sea verdadera.

Aun cuando las estimaciones por intervalos y las pruebas de hipótesis puedan parecer muy distintos, hay en realidad una asociación muy estrecha y el intervalo de confianza permite inferir el resultado de un test de hipótesis al nivel de significancia dado. En la Figura 1 basada en el primer ejemplo, se puede ver la diferencia de presión arterial entre dos grupos. Los intervalos de confianza permiten ver la precisión de la estimación de la diferencia hecha con la muestra. La ausencia de diferencia es la hipótesis nula y si el intervalo de confianza 95% incluye este valor implica que no hay evidencia suficiente para rechazar la hipótesis nula al nivel de confianza dado.

Igual cosa sucede cuando se presentan los intervalos de confianza de un riesgo relativo o de una razón de ventajas. En estos, la hipótesis nula es que no existe diferencia en el riesgo entre los grupos. Así, cuando un intervalo de confianza de un riesgo relativo incluye a 1 significa que no existe suficiente evidencia, para rechazar la hipótesis nula. Por ejemplo, el riesgo relativo de tener dolor lumbar de parturientas que recibieron una anestesia epidural, comparadas con aquellas que no, es de 1,76 al primer día y de 2,22 a las 6 semanas. Los intervalos de 95% de confianza fueron de 1,06 a 2,92 y de 0,89 a 5,53 respectivamente. Estos permite inferir que la P es < 0,05 en el primer día, pues no incluye a 1, y que es > a 0,05 en la sexta semana pues sí lo hace. Además, se puede agregar que la imprecisión de la estimación es mayor a las seis semanas.

Otra utilidad de los intervalos de confianza es la estimación visual de la importancia de un resultado determinado, observando la precisión de la estimación en relación con una diferencia que se considere relevante (Figura 2).

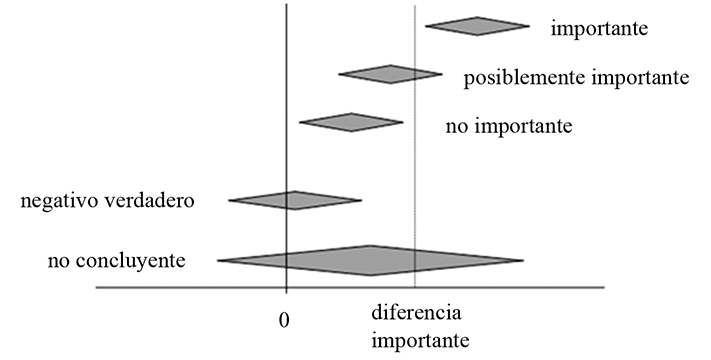
Figura 2 Otro uso de los intervalos de confianza con posibles conclusiones frente a diferencias, la precisión de la estimación y el tamaño de la muestra graficada con la dimensión del rombo. (Modificado de Armitage & Berry, 1997).

De lo expuesto en este artículo y en el anterior, fluye que para permitir una adecuada interpretación por parte de los lectores, los trabajos debieran comunicar los valores reales encontrados, el valor exacto de P y no sólo el insuficiente < 0,05, la indicación si la prueba de hipótesis se hizo de una o dos colas y los intervalos de confianza de las estimaciones puntuales. Calcular y comunicar la potencia del test o del experimento es indispensable cuando los resultados aparecen como no significativos: es deber de los autores hacerlo y de los lectores exigirlo.

INTERVALO DE CONFIANZA Y UN CASO ESPECIAL DE ERROR TIPO II: CERO EN EL NUMERADOR

Muchos trabajos evalúan algún aspecto de un procedimiento o de un tratamiento y además presentan la incidencia de los efectos adversos o la morbimortalidad. Con eventos que tienen una baja incidencia, es frecuente que en una serie no existan casos del evento y se concluye que tal procedimiento o tratamiento carece de efectos adversos o bien que aparece como seguro. Si bien ese cero es la mejor estimación que podemos hacer de la ocurrencia del fenómeno que nos interesa, nada nos dice de la imprecisión de la estimación. La estimación de intervalo es de gran ayuda para dimensionar esa incertidumbre y evaluar adecuadamente las cifras. Hanley, en un trabajo con el sugerente título de “Si nada resulta malo, ¿está todo bien?”, propone un método aproximado pero muy simple para estimar el límite superior de ese intervalo, ya que el inferior es igual a cero: la regla del 3 o del 5. Con muestras superiores a 20 las cifras obtenidas son bastante cercanas a aquellas calculadas con mayor precisión.

Límite inferior Límite superior

0% 3/n, con 95% de confianza

0% 5/n, con 99% de confianza

n = tamaño de la muestra

Por ejemplo, un trabajo evalúa el efecto de un nuevo anestésico en 42 pacientes, caracterizando la latencia y duración. El trabajo concluye que actúa rápido, tiene una corta duración y que es seguro porque no hubo efectos adversos. Con la regla del 3 o del 5 es posible estimar que el límite de confianza superior para la incidencia de efectos adversos es de 7,14% con un 95% de confianza y de 11,9% con un 99% de confianza. En la Tabla 1 hemos resuelto los límites de confianza superiores para distintos tamaños de estudios con cero en el numerador. Es aparente que si se están estudiando fenómenos de baja incidencia, las casuísticas no pueden ser de tamaños limitados.

Tabla 1 Límites de confianza superiores en relación al tamaño de la muestra cuando el inferior es igual a 0%, calculados con la regla del 3 ó 5

REFERENCIAS

1. Altman DA, Machin D, Bryant T, Gardner M (editors). Statistics with confidence. 2nd ed. London: BMJ Books, 2000.
2. Altman DG, Bland JM. Absence of evidence is not evidence of absence. BMJ 1995; 311: 485.
3. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
4. Armitage P, Berry G. Estadística para la investigación biomédica. 3a ed. Harcourt Brace: Barcelona, 1997.
5. Bland JM, Altman DG. Transformation, means, and confidence intervals. BMJ 1996; 312: 1079.
6. Bland M. An Introduction to Medical Statistics. 3rd Ed, Oxford: OUP, 2006.
7. Cumming G. Inference by Eye: Pictures of Confidence Intervals and Thinking About Levels of Confidence. Teaching Statistics 2007; 29: 89-93.
8. Dawson-Saunders B, Trapp RG. Bioestadística Médica. México D.F: Manual Moderno, 1993.
9. Emerson JD, Colditz GA. Use of statistical analysis in the New England Journal of Medicine. En Bailar III JC, Mosteller F. Medical uses of Statistics. (2nd ed). Boston: NEJM Books, 1992.
10. Glantz SA. Primer of Biostatistics. 3a edición, New York: McGraw-Hill, 1992.
11. Guyatt G, Jaeschke R, Heddle N, et al. Basic Statistics for Clinicians: 2. Interpreting Study Results: Confidence Intervals. Can Med Ass J 1995; 152: 169-173.
12. Hanley JA, Lippman-Hand A. If nothing goes wrong, is everything all right? JAMA 1983; 249: 1743-1745.
13. Macarthur A, Macarthur C, Weeks S. Epidural anaesthesia and low back pain after delivery: a prospective cohort study. BMJ 1995; 311: 1336-1339.
14. Portney LG, Watkins MP. Foundations of Clinical Research. Applications to practice. 2nd ed. Upper Saddle River: Prentice-Hall, 2000.
15. Sim J, Reid N. Statistical Inference by Confidence Intervals: Issues of Interpretation and Utilization. Phys Ther 1999; 79: 186-195.