MEDIDAS DE POSICIÓN CENTRAL Y DE DISPERSIÓN

Jorge Dagnino S. ¹

Rev. chil. anest. Vol. 43 Número 2 pp. 112-115|https://doi.org/10.25237/revchilanestv43n02.07 PDF|ePub|RIS

• Para resumir datos de escalas nominales se usa la frecuencia relativa y la tasa.

• Cuando la variable tiene una distribución normal, se usa la media y la varianza o desviación estándar como medidas de posición central y de variabilidad respectivamente.

• Si la distribución no es normal, se usa la mediana y los percentiles como medidas de posición central y variabilidad respectivamente.

Cuando un investigador recoge información generalmente lo hace con una o dos ideas en mente: obtener información descriptiva sobre la población desde la cual se eligió la muestra o probar algunas hipótesis sobre esa población. En este artículo nos concentraremos en las distintas maneras de resumir los datos recolectados de una variable cualquiera de manera que describa, de la mejor manera posible, la muestra estudiada y el universo de donde se tomó la muestra y que no ha sido observado. La manera de hacerlo dependerá del tipo de datos y de su escala de medición.

RESUMEN DE LOS DATOS DE ESCALAS NOMINALES

Los datos nominales se resumen estableciendo una relación entre el número de individuos que presentan una característica y el número total de individuos que constituyen la muestra o población.

1) Frecuencia relativa: es la relación entre el número de individuos que en un momento determinado presentan la característica y el número total de los individuos que constituyen la muestra. Para calcularla es necesario saber el número de individuos que positivamente se sabe presentan la característica y el de aquellos que positivamente no la presentan. Muchas veces se desconoce lo que le sucedió a una parte de la muestra, por errores de muestreo o pérdidas en el seguimiento, ignorando si presentaron o no la característica de interés; cuando esta proporción de desconocidos sube del 10% del total, la precisión de la frecuencia relativa obtenida empieza a sufrir pues no siempre se puede deducir que las proporciones en este grupo serán similares a la de los efectivamente observados. Un ejemplo de esto se dio en una revisión retrospectiva de mortalidad perioperatoria en ancianos que arrojó una frecuencia mucho menor que la evaluación prospectiva y ello porque en los pacientes que habían fallecido había una mucho mayor proporción de fichas extraviadas y por lo tanto sin seguimiento.

2) Tasas: por comodidad se amplifica, multiplicando por 100, el valor de la frecuencia relativa para convertirlo en números enteros, y en vez de calcularla para un instante se hace para un lapso determinado. Estos valores se emplean en epidemiología y demografía para conocer los cambios de frecuencias de un evento en una localidad y en un lapso determinado. Por ello, cada vez que se cita este valor debe necesariamente indicarse el lugar y el período que comprenden. Hay tasas brutas (relacionan la característica con toda la población a la cual pertenecen los individuos: mortalidad en Chile en 2014), específicas (cuando el acontecimiento o la población están especificadas: mortalidad de una enfermedad, mortalidad infantil o en ancianos) y ajustadas. Dentro de las tasas específicas se ubican las tasas de letalidad de una enfermedad (amplificación por 100 del número de defunciones por esa enfermedad dividido por el número de pacientes que la han sufrido) y las tasas de prevalencia (amplificación por 100 del número del total de casos de una enfermedad, en una población definida y en un momento dado, dividido por el número de individuos que constituyen la población).

RESUMEN DE LOS DATOS DE ESCALAS CUANTITATIVAS

Los datos en una escala cuantitativa pueden ser resumidos mediante valores centrales, que indican la magnitud a la cual corresponde el centro de la distribución, junto con medidas de dispersión de los valores individuales con respecto al valor central.

• I. Valores centrales

1) Media o Promedio: (Del latín, pro medio: punto en que una cosa se divide por la mitad o casi la mitad). Matemáticamente es el número que resulta al efectuar una serie determinada de operaciones con un conjunto de números y que en determinadas condiciones puede representar por si sólo a todo el conjunto. Recibe distintas denominaciones según las operaciones que se realicen para calcularla.

1. Media aritmética: suma de los valores individuales dividida por el número de ellos. Su mayor desventaja es que es muy sensible a los valores extremos (outliers); por ejemplo, la media de 16, 18, 20, 22 y 24 es 20 y en realidad 20 parece representar adecuadamente estos números; la media de 1, 2, 3, 4 y 90 también es 20 pero es obvio que ésta no representa adecuadamente el conjunto.

2. Media geométrica: raíz enésima del producto de n números. Alternativamente se calcula el logaritmo de cada valor, luego la media aritmética de éstos y luego se saca el antilogaritmo. Se usa para datos que tienen un rango muy amplio o en general en todo fenómeno en que la variable crezca exponencialmente: microbiología y muchos resultados de análisis bioquímicos. También para el análisis de curvas dosis-respuesta.

3. Media ponderada: a cada uno de los valores individuales del cálculo se le asigna un determinado peso que depende de su importancia relativa de acuerdo con algún criterio establecido.

4. Otras medias de rara aplicación en biología: armónica (recíproco del promedio de los recíprocos), cuadrática (raíz cuadrada del promedio de los valores elevados al cuadrado).

2) Mediana: valor que ocupa el lugar central cuando los datos están ordenados. Cuando el total de datos es par, se usa el promedio de los dos valores centrales. Se usa con datos cuantitativos o con cualitativos ordinales, pero no tiene sentido con datos cualitativos no ordinales que precisamente carecen de un orden que permita determinar la mediana. Tiene la ventaja que no es sensible a los valores extremos. En el ejemplo usado para la media, la mediana de 16, 18, 20, 22 y 24 es igual a la media, 20; la mediana de 1, 2, 3, 4 y 90 es 3, número que representa mejor al conjunto de datos que la media que es 20.

3) Modo o Moda: número, clase o intervalo que tiene mayor frecuencia en la muestra. Estrictamente, sin embargo, conviene definirla como aquel o aquellos valores, clases o intervalos de clases que tienen mayor frecuencia que sus adyacentes. Con esta definición, es posible encontrar distribuciones bimodales o incluso con más modas. En la distribución de la Figura 1, la primera definición sólo aceptaría una moda; estas distribuciones son frecuentes como por ejemplo diversos fenómenos circadianos. Sólo tiene sentido usar la moda cuando se tiene un número grande de datos que, si son continuos, deben estar agrupados en intervalos de clase.

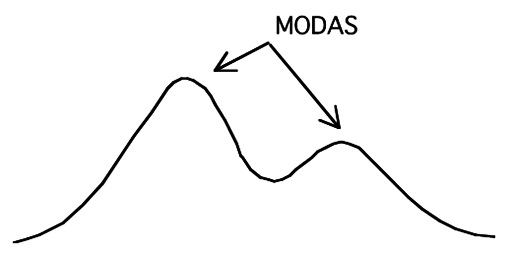
Figura 1 Distribución bimodal.

• II. Medidas de dispersión

Una vez determinado el valor que caracterizará el centro de la muestra, se hace necesario describir la dispersión de los valores en torno a ella.

1) Margen de variación: recorrido, rango o amplitud. Corresponde a la diferencia entre valores máximos y mínimos en una distribución. Tiene la ventaja de expresarse en las mismas unidades que los datos originales y ser fácil de calcular. Su desventaja es que sólo considera a dos datos en el cálculo por lo que su uso es restringido a cuando se quiere una medida rápida de la dispersión de la muestra.

2) Varianza: Si los datos tienen una distribución aproximadamente normal, para definir una medida de dispersión en que participen todas las observaciones de la muestra se puede usar la distancia (desviación) entre cada dato y la media siendo el promedio de esas desviaciones una medida de la dispersión. El problema es que la mitad de los valores serán negativos con respecto a la media y la otra mitad serán positivos resultando el promedio con un valor de cero o cercano a él. En el primer ejemplo, el cálculo sería de (-4)+(-2)+0+(+2)+(+4)= 0 (el resultado de sumar las diferencias de 16-20, 18-20, 20-20, 22-20 y 24-20). El error aquí es considerar a las distancias con un valor negativo cuando en realidad todas son positivas en términos absolutos. Una salida es usar solo estos valores absolutos de las diferencias pero esto complica las matemáticas de los cálculos posteriores. Por ello se recurre a elevar las distancias al cuadrado con lo que se eliminan los negativos; en el ejemplo, 16+4+0+4+16. Para estimar la varianza del universo se divide por N, el número de individuos y para calcular la de la muestra se divide por n-1. La unidad de la varianza es el cuadrado de la unidad de la variable en cuestión: por ejemplo, la varianza de los pesos será en kg2 y la de las alturas será expresada en cm2 o m2.

3) Desviación estándar o típica: Para no trabajar con cifras al cuadrado, se saca la raíz cuadrada de la varianza resultando en la desviación estándar. Es importante destacar que tanto la varianza como la desviación estándar toman a la media como centro al calcular la dispersión y que la media y la varianza o la desviación estándar, por sí solas, describen completamente a una distribución normal, pero solo a una distribución normal. A la media y a la desviación estándar se les denomina parámetros y a las pruebas de inferencia que las utilizan en su desarrollo se les denomina paramétricas (por ejemplo, t de Student, ANOVA). Como no describen matemáticamente a distribuciones que no son normales no deben usarse en estos casos pues carece de sentido hacerlo (por ejemplo, promedio de clasificación ASA), ni tampoco usar las pruebas paramétricas para hacer inferencias acerca de variables que siguen esas distribuciones.

4) Coeficiente de variación: es la desviación estándar expresada como porcentaje de la media aritmética. Sirve para expresar y comparar la variabilidad relativa en dos conjuntos de valores expresados en unidades diferentes. Asume que la desviación estándar es proporcional a la media lo que no siempre es así.

5) Cuartiles, deciles y percentiles: representan la división de la distribución por aquellos valores que la dividen en una determinada proporción. Los valores que la dividen en cuartas partes se denominan cuartiles; en décimas partes, deciles; en centésimas partes, percentiles. Se emplean en aquellos casos en que se usó la mediana como parámetro de posición central (Figura 2).

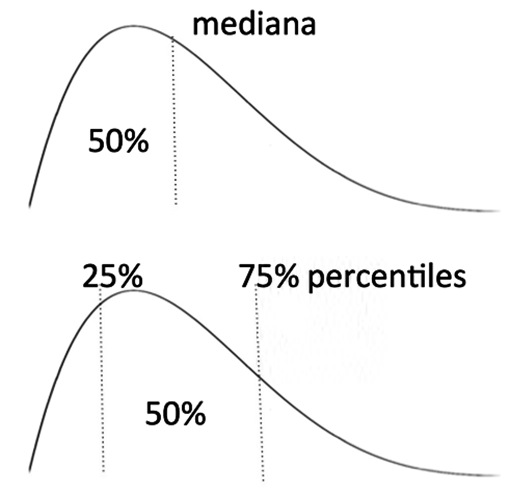
Figura 2 La mediana divide a la población en dos mitades, mientras que los percentiles 25 y 75 encierran entre ellos también a la mitad de la población y dejan por fuera 25% a cada lado.

Las relaciones que existen entre las distintas medidas de posición central en una distribución normal y cuando no lo es se aprecian en la Figura 3. En una distribución normal, la media, la mediana y el modo son coincidentes. Cuando la distribución no es normal, las medidas de distribución central difieren entre sí, diferencia que será mayor mientras mayor sea la divergencia con una distribución normal. Si la media es mayor que la mediana la distribución está sesgada hacia la derecha y si es menor que la mediana está sesgada a la izquierda.

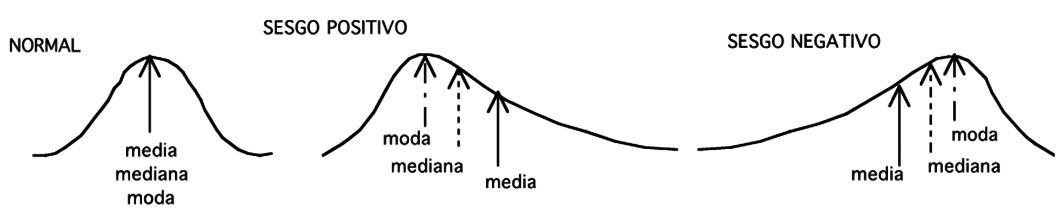
Figura 3 Medidas de posición central y distribución. Se observa coincidencia de la media, mediana y moda cuando la distribución es normal y diferencias entre ellas cuando la distribución es sesgada.

En la Figura 3 se puede ver gráficamente que las medidas de dispersión paramétricas pierden su capacidad descriptora en una distribución sesgada: al restar dos desviaciones estándares de la media calculada podemos obtener cifras negativas cuando en la realidad no pueden serlo. Por ejemplo, cuando el tiempo de despertar después del fin de una anestesia tiene una media de 4,5 minutos y 3,9 de desviación estándar, producto de unos pocos pacientes que tomaron mucho tiempo en despertar aunque la mayoría lo hicieron dentro de los primeros 10 minutos (sesgo positivo); usar estos parámetros implicaría que parte de los pacientes nunca se durmieron pues “despertaron” antes de iniciar la anestesia (lo que causaría gran placer a algunos con aquella definición de anestesista como “alguien semidormido cuidando a un paciente semidespierto…”).

La correspondencia entre las distintas medidas de dispersión, percentiles y desviaciones estándar, cuando una distribución es normal, han sido dibujadas en la Figura 4. Los percentiles 2,5 y 97,5 coinciden aproximadamente con dos desviaciones estándar por debajo y por arriba de la media respectivamente, cifras que vale la pena retener para cuando se hable de inferencias y umbrales de significación.

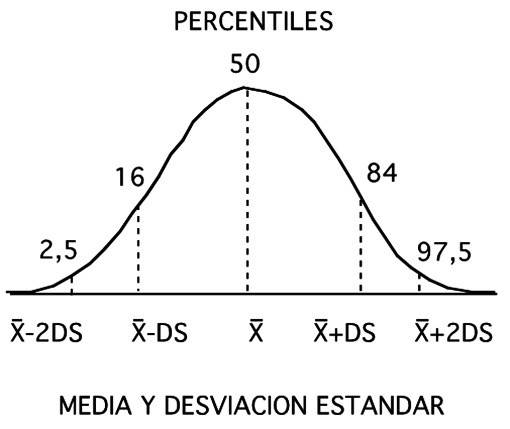
Figura 4 Correspondencia entre percentiles y desviaciones estándar medidas desde la media.

En general, se puede decir que cuando el valor de una variable en un individuo dado tiene mayor probabilidad de estar cerca del valor del promedio de los valores de todos los individuos de esa población y con igual probabilidad de estar por sobre o por debajo de esa cifra, entonces se debe usar la media y la desviación estándar. Cuando el valor de la variable tiene mayor probabilidad de caer bajo o sobre la media entonces es mejor usar la mediana y por lo menos dos otros percentiles.

ERROR ESTÁNDAR DE LA MEDIA

No es una estimación de ninguna cantidad en la población por lo que no debe usarse como una representación de la variabilidad de la muestra. Si se menciona en este artículo es precisamente para recalcar esto, pues es un error que se comete con frecuencia, a veces premeditadamente. El error estándar de la media es un número hipotético que cuantifica la certeza con que la media que hemos obtenido en una muestra aleatoria representa la verdadera media de la población desde la cual tomamos la muestra. Esta certeza aumenta en la medida que aumenta el tamaño de la muestra y por lo tanto el error estándar de la media disminuye en la medida que es mayor el n de la muestra aun cuando la varianza permanezca igual. Es posible calcular el error estándar de cualquier estadístico (definido como cualquier medida cuantitativa derivada o calculada en una muestra) y no sólo de la media como veremos posteriormente en los cálculos y conceptos sobre intervalos de confianza.

REFERENCIAS

1. Altman DG, Gore SM, Gardner MJ, Pocock SJ. Statistical guidelines for contributors to medical journals. Br Med J 1983; 286: 1489-1493.
2. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
3. Bland M. An Introduction to Medical Statistics. 3rd Ed, Oxford: OUP, 2006.
4. Dawson-Saunders B, Trapp RG. Bioestadística médica. México D.F: Manual Moderno, 1993.
5. Feinstein AR. On central tendency and the meaning of mean of pH values. Anesth Analg 1979; 58: 1-3.
6. Glantz SA. Primer of Biostatistics. 3a edición, New York: McGraw-Hill, 1992.
7. Portney LG, Watkins MP. Foundations of Clinical Research. Applications to practice. 2nd ed. Upper Saddle River: Prentice-Hall, 2000.