MEDIDAS REPETIDAS Y MEDIDAS SUMATIVAS

Jorge Dagnino S. ¹

Rev. chil. anest. Vol. 43 Número 4 pp. 313-316|doi:
PDF|ePub|RIS

• Las mediciones seriadas son frecuentes en investigación médica.

• El análisis de este tipo de datos presenta diversas dificultades en su ejecución e interpretación por lo que se aconseja la intervención de un estadístico profesional si se recurre a análisis complejos.

• Las medidas sumativas, sin embargo, son relativamente fáciles de analizar e interpretar sin perder discriminación ni potencia.

• Idealmente deben estar incorporadas en el protocolo del estudio, puede ser una o varias, y deben estar sugeridas por el o los objetivos del estudio.

• Ejemplos de medidas sumativas son: promedio de la respuesta, área bajo la curva de la respuesta, valores extremos alcanzados.

Los estudios que envuelven mediciones repetidas o seriales para averiguar o predecir la evolución de una o más variables a lo largo del tiempo son frecuentes en medicina. Por ejemplo, variaciones de la concentración plasmática de una droga luego de su administración enteral o parenteral o la evolución del dolor en el postoperatorio inmediato. A veces se trata de un grupo de sujetos, habitualmente con fines descriptivos, y otras de dos o más grupos, generalmente para comparar respuestas luego de una intervención o en grupos que difieren por alguna razón de interés (por ejemplo sanos y enfermos).

Se distingue para estos efectos dos tipos de respuesta: de extremos (peaked, de máximo o mínimo) y de crecimiento (o decrecimiento). En la primera, el extremo de interés se alcanza durante la duración de la observación y luego los valores regresan a la basal; en estos estudios generalmente interesa conocer el máximo alcanzado, el tiempo en alcanzarlo, el número de individuos que lo alcanzan o no lo alcanzan, o el tiempo en caer bajo un mínimo o umbral. En cambio, en las respuestas de crecimiento, la variable aumenta o disminuye durante el período de estudio, sin necesariamente alcanzar un máximo o un mínimo y sin regresar a los valores basales; aquí el interés está en la velocidad de cambio. Por ejemplo, aumento de la estatura en el primer año de vida.

El análisis de dichos datos no siempre es evidente y presenta diversas dificultades a veces no advertidas en la literatura; por este motivo, frecuentemente es inadecuado y puede fracasar en responder la pregunta clínica relevante planteada directamente y/o puede ser estadísticamente inválido. Por ejemplo, una de las alternativas más comunes, y equivocada en los dos aspectos mencionados, ha sido la de comparar la evolución de los grupos en cada punto de tiempo con comparación de medias como por ejemplo un test t de Student repetido; ahondando en el error, los resultados se grafican usando los promedios de cada grupo en cada tiempo de observación, se ponen asteriscos como significación estadística y se añaden barras de error (no siempre identificadas como error estándar o desviación estándar) (Figura 1).

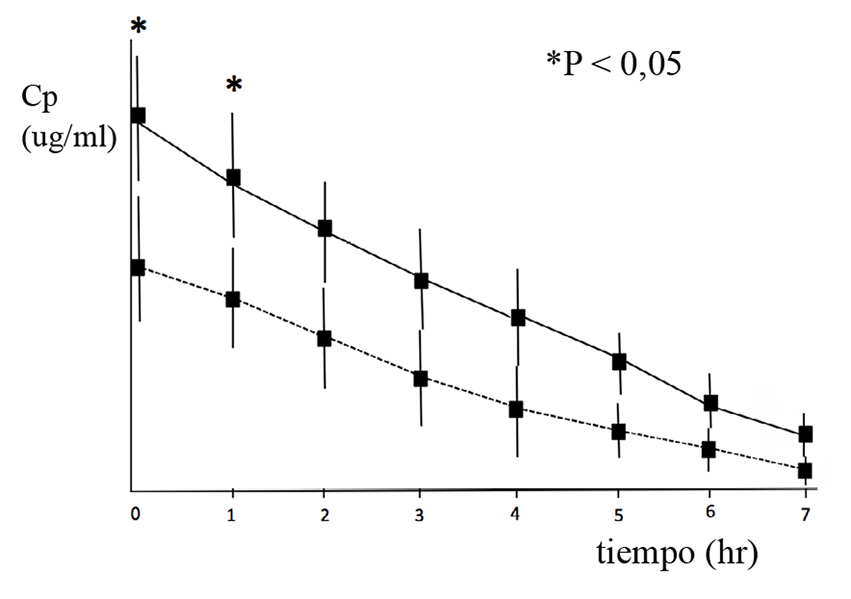
Figura 1 Caída de la concentración plasmática (Cp) en dos grupos luego de la administración intravenosa.

Esta aproximación tiene diversos problemas: la curva promedio podría no ser, y frecuentemente no lo es, un buen descriptor de las curvas individuales de cada sujeto por lo que puede ocultar información importante pues el interés puede estar en las respuestas individuales; los máximos y mínimos de las respuestas individuales muchas veces no coinciden en el tiempo por lo que los promedios tienden a ocultar estas variaciones y, a la vez, a aumentar la variabilidad entre los individuos en cada punto de muestreo (Figura 2). Otro problema es que los datos en cada punto de tiempo están claramente relacionados con los datos que les anteceden y suceden por lo que no corresponde analizarlos como independientes. Por este mismo motivo, la separación entre significativos y no significativos es artificial.

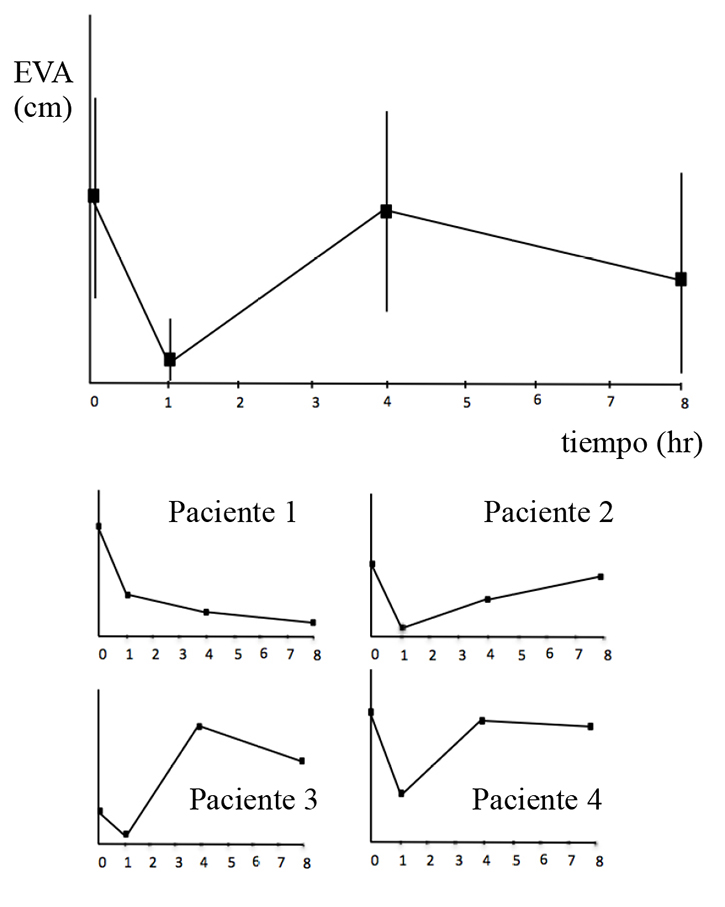
Figura 2 Evolución del dolor postoperatorio en un grupo de pacientes con promedios y DE al llegar a recuperación y luego a la 1, 4 y 8 horas. En la parte inferior, curvas individuales de 4 pacientes donde se ve evoluciones diferentes a lo largo del tiempo.

Las alternativas para analizar este tipo de datos son varias donde muchas veces el método más usado depende de la disciplina. Las recomendaciones expertas también han ido cambiando y existe actualmente mucha controversia sobre cuál o cuáles alternativas son mejores y en qué circunstancias. El debate y raciocinios pueden llegar a ser muy técnicos y complejos por lo que seguirlos y llegar a una decisión independiente es muy difícil o imposible para quien no es un estadístico profesional. Por ello, si se quiere usar estos métodos se debe consultar a uno de estos profesionales, una vez más, ojalá desde la etapa de diseño del estudio. Usar los programas disponibles puede generar errores importantes al desconocer cuáles son los supuestos de cada aproximación, sus limitaciones y si la estructura de la investigación cumple tal o cual requisito. Para el lector crítico, como sucede en los análisis más complejos de variable múltiple, conviene buscar entre los autores o entre los agradecimientos la presencia de un estadístico profesional; si no los encuentra y no hay una discusión sobre las razones de la elección del método usado y de sus limitaciones y posibles errores, entonces hay que tomar los resultados con beneficio de inventario pues pueden ser meramente el resultado de un programa de computación y no de un raciocinio científico.

Los siguientes métodos en orden creciente de complejidad están entre las alternativas: ANOVA para medidas repetidas, ANOVA de multivariables (MANOVA), el método de Kenward y Roger que es una modificación de F, y los llamados modelos jerárquicos. Estos métodos tienen diversos problemas en su aplicación e interpretación; para muchos estadísticos médicos, los dos primeros métodos tendrían inconvenientes insalvables en la mayoría de los casos, por lo que no debieran ser usados en este tipo de estudios. Entre el método de Kenward y Roger y los métodos jerárquicos, estos últimos serían preferibles. Como alternativa a estos métodos, están las medidas sumativas y existe consenso en que estas son la mejor elección en la mayoría de los casos, por su relativa facilidad de cálculo, aplicación e interpretación y porque en el análisis no perderían discriminación ni potencia.

Las medidas sumativas (summary measures) fueron propuestas hace más de 70 años, pero son relativamente poco usadas en la investigación médica, a pesar de sus ventajas (Tabla 1). El método consta de dos etapas: en la primera se genera una medida sumativa (por ejemplo, el área bajo la curva o ABC) de cada individuo; en la segunda, se analizan estas medidas sumativas de cada individuo como si fuesen valores individuales con métodos habituales de comparación como, por ejemplo, test t de Student o U de Mann-Whitney.

Tabla 1 Listado de posibles medidas sumativas

El punto más importante reside en la elección de cuál o cuáles medidas sumativas usar, lo que no siempre es evidente. Aquí la primera consideración es que dependerá de la pregunta que el estudio quiere responder; de hecho su elección debe ajustarse al objetivo perseguido. A continuación, en la Tabla 2, se resumen algunas medidas propuestas por Matthews y colaboradores en 1990.

Tabla 2 Medidas sumativas según el tipo de respuesta (Modificada de Matthews y cols.)

Las medidas sumativas tienen diversas ventajas entre las que se pueden mencionar las siguientes:

• Son conceptualmente simples y usan test estadísticos simples y comunes.

• Tienen validez estadística.

• Son relativamente fáciles de calcular e interpretar y pueden ser usadas cuando los intervalos de tiempo son desiguales.

• Son robustas ante datos faltantes y pueden ser elegidas de manera de responder un rango de preguntas.

• Puede ser mejor usar más de una. Por ejemplo, el promedio y la mínima o máxima.

• Se puede usar en el contexto de una regresión múltiple, donde se usa una medida sumativa como la variable de resultado y otros factores individuales son predictoras. Por ejemplo: la variable de resultado isquemia postoperatoria representada como el área bajo la curva de desniveles ST en las primeras 24 horas del postoperatorio.

Algunas consideraciones generales para quienes decidan usarlas como alternativa en un trabajo que están planeando o al analizar su uso al leer un trabajo publicado:

• Considerarlas y decidirlas en la etapa de diseño aunque exploratoriamente podría ser post hoc. Hacerlo tempranamente tiene la ventaja de que se puede elegir el muestreo que mejor respuesta entregue. Por ejemplo, si lo que interesa es el máximo, se decide tomar muestras más frecuentes en torno a ese momento.

• Se puede usar más de una pero deben ser plausibles biológicamente. Si bien no hay un máximo sugerido, habitualmente no son más de tres o cuatro las necesarias.

• Se sugiere dibujar curvas individuales. También usar métodos habituales como histogramas o “nube de puntos” que pueden descubrir relaciones o diferencias que no son aparentes en un gráfico de los valores individuales.

El cálculo del área bajo la curva puede hacerse de diversas maneras y existen programas que pueden hacer el cálculo sin dificultades. Otra alternativa es el método de los trapezoides (Figura 3) que consiste en sumar segmentos discretos de la curva multiplicando la altura (usando el promedio de las dos alturas) por el ancho. La precisión de la estimación del área bajo la curva y también de la variable de interés aumenta con un muestreo más frecuente.

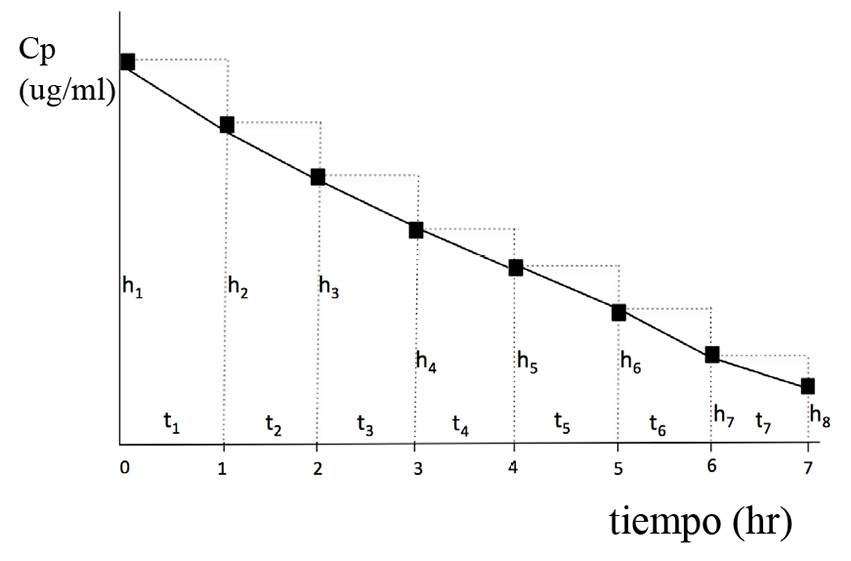
Figura 3 Cálculo del área bajo la curva (ABC) usando el método de los trapezoides donde ABC = [(H₁+H₂)/2)*t₁)]+[(H₂+H₃/2)*t₂)]… +[(H₇+H₈)/2)*t₇)]. h₁ a h₈ representan las alturas de los trapezoides y t1 a t7 el ancho de cada uno; en este caso los intervalos son iguales. En el cálculo de cada segmento, se usa el promedio de las alturas.

El método también se puede usar cuando las mediciones son irregulares como en el ejemplo de la Figura 4.

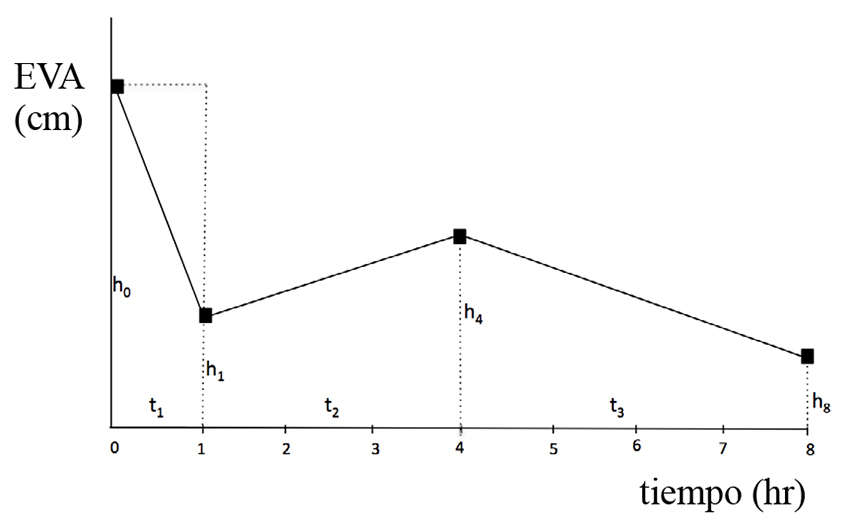
Figura 4 Área bajo la curva (ABC) de dolor postoperatorio medido con una escala visual análoga (EVA) en un individuo al llegar a recuperación (t₀) y luego a las 1, 4 y 8 horas. Aquí: ABC = [(H₀+H₁)/2)*t₁)]+ [(H₁+H₄/2)*t₂]… +[(H₄+H₈)/2)*t₃)].

REFERENCIAS

1. Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
2. Armitage P, Berry G. Estadística para la investigación biomédica. 3a ed. Barcelona: Harcourt Brace, 1997.
3. Everitt BS. The Analysis of Repeated Measures: A Practical Review with Examples. The Statistician 1995; 44: 113-135.
4. Frison L, Pocock SJ. Repeated Measures in Clinical Trials Analysis Using Mean Summary Statistics and its Implications for Design. Statist Med 1992; 11: 1685-1704.
5. Lambert PC, Burton PR, Abrams KR, Brooke AM. The analysis of peak expiratory flow data using a three-level hierarchical model. Statist Med 2004; 23: 3821-3839.
6. Matthews JNS, Altman DG, Camp-bell MJ, Royston P. Analysis of serial measurements in medical research. BMJ 1990; 300: 230-235.
7. Omar RZ, Wright EM, Turner RM, Thompson SG. Analysing Repeated Measurements Data: A Practical Comparison of Methods. Statist Med 1999; 18: 1587-1603.
8. Peacock J, Peacock PJ. Oxford Handbook of Medical Statistics. Oxford: OUP, 2011.
9. Senn S, Stevens L, Chaturvedi N. Repeated measures in clinical trials: simple strategies for analysis using summary measures. Statist Med 2000; 19: 861-877.
10. Sullivan LM. Repeated measures. Circulation 2008; 117: 1238-1243.
11. Vickers AJ. How many repeated measures in repeated measures designs? Statistical issues for comparative trials. BMC Medical research Methodology 2003; 3: 22.
12. Vossoughi M, Ayatollahi SMY, Towhidi M, Ketabchi F. On summary measure analysis of linear trend repeated measures analysis: performance comparison with two competing methods. BMC Medical Research Metodology 2012; 12: 33.