Jorge Dagnino S. 1
Rev. chil. anest. Vol. 43 Número 4 pp. 317-321|doi:
PDF|ePub|RIS
-
Riesgo relativo (RR) y odds ratio (OR) son dos maneras de explorar la relación entre dos variables dicotómicas.
-
El RR se usa fundamentalmente en la evaluación de trabajos prospectivos mientras que el OR se usa principalmente en el análisis de trabajos retrospectivos.
-
En el análisis de eventos infrecuentes, el OR puede interpretarse razonablemente como riesgo. Sin embargo, en eventos frecuentes o con OR elevados, el OR puede sobrestimar demasiado el RR por lo que no debe ser interpretado como una medida de riesgo.
-
Con ambos, siempre deben calcularse y comunicarse los intervalos de confianza como estimación de la precisión alcanzada.
Hay diversas maneras de analizar una tabla de 2 x 2 en la que se comparan dos grupos en relación a la ocurrencia de algún evento. En otro artículo se discutió el uso del 2 y del test exacto de Fisher para estos efectos. Estas pruebas de hipótesis permiten estimar las probabilidades de que la hipótesis nula en relación con dicha tabla sea verdad; en otras palabras, cuál es la probabilidad que las cuatro celdas de la Tabla 2 x 2 contengan los mismos números, de que no exista diferencia entre los grupos. En relación con el riesgo de algún evento, sin embargo, interesa tener además un número que permita cuantificar la magnitud de la diferencia: el riesgo relativo y el odds ratio o razón de ventajas son las dos medidas más comunes en la literatura biomédica. Al igual que en otras circunstancias, los límites de confianza permiten hacer estimaciones respecto de la probabilidad de que la hipótesis nula sea verdadera y, además, hacer un juicio sobre la precisión de la estimación puntual; por ello, siempre deben ser calculados y comunicados en trabajos que usen riesgo relativo u odds ratio.
RIESGO RELATIVO
Se usa principalmente en el análisis de trabajos prospectivos en los cuales dos grupos son seguidos para determinar la ocurrencia de algún evento. En cada grupo, el riesgo de ocurrencia de dicho evento se obtiene dividiendo el número de casos con el resultado de interés por el número total de casos. La razón entre estas proporciones en cada grupo es una medida del riesgo de un grupo comparado con el otro y se denomina riesgo relativo (RR). La interpretación del RR es intuitiva: un RR de 2 expresa que el riesgo en un grupo es el doble que en el otro grupo. Como veremos, no existe una interpretación cuantitativa simple del OR excepto cuando es aproximadamente igual al RR.
La Tabla 2 x 2 que se genera en esta situación es así:
|
Grupo 1 |
Grupo 2 |
||
| Resultado se presenta |
a |
b |
a + b |
| Resultado no se presenta |
c |
d |
c + d |
|
a + b |
b + d |
Total |
El riesgo de cada grupo es a/(a+c) y b/(b+d) respectivamente, por lo que el riesgo relativo es igual a la razón entre ambos riesgos [(a/(a+c)]/[(b/(b+d)]. Se define como el cociente de las probabilidades de tener la enfermedad o presentar el resultado de interés si está presente o ausente el factor predictivo, el factor de riesgo. Como con otras estimaciones puntuales, también es posible calcular un intervalo de confianza para el riesgo relativo usando las siguientes fórmulas, partiendo por el cálculo del error estándar (EE):
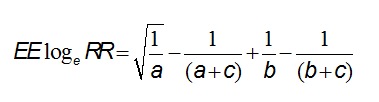
La distribución de logeRR es Normal por lo que se puede calcular un intervalo, por ejemplo 95%, como:
loge RR – [N (1- /2) •EE( log e RR )] a log e RR + [N (1- /2) •EE( log eRR)]
Recordemos que para un IC95 , N ( 1- /2) o N 0,975 es el percentil que deja afuera el 2,5% del área bajo la curva en un extremo y el 2,5% en el otro extremo. Los valores están disponibles en tablas en todos los textos de estadística y en páginas electrónicas. N 0 ,975 es igual a 1,96 y N0,95 a 1,645 (dejando el 10% de la curva, la mitad en cada extremo, fuera de esos límites). El intervalo de confianza se obtiene a través del antilogaritmo de estos valores (ver ejemplo).
La hipótesis nula, que plantea que no hay diferencias entre los grupos, significa que el RR es igual a 1. Un RR mayor de 1 significa un aumento, y uno menor de 1, una disminución del RR. Por lo tanto, cuando el intervalo de confianza incluye a 1, la diferencia de riesgo no es estadísticamente significativa. Como siempre, el intervalo de confianza depende del tamaño de la muestra.
EJEMPLO DE RIESGO RELATIVO
Un trabajo compara la morbimortalidad perioperatoria en un grupo que recibió un bloqueador beta-adrenérgico en el perioperatorio comparado con la de un grupo control que recibió cuidados estándares. Dos de 61 pacientes en el grupo con bisoprolol y 9 de 62 pacientes sin el bloqueador beta-adrenérgico murieron de causa cardiaca:
|
Casos |
Controles |
||
| Muertos |
2 |
9 |
11 |
| Vivos |
59 |
53 |
112 |
|
61 |
62 |
123 |
El riesgo de morir por una causa cardiaca de los casos es de 2/61 = 3,28% y el de los controles es de 9/62 = 14,52%; riesgo relativo es, entonces, de 3,28/14,52 = 0,226. La información puede leerse como que el riesgo de muerte de causa cardiaca en los pacientes tratados con bisoprolol se redujo al 22,6% del riesgo de los pacientes con un cuidado estándar.
El cálculo del IC95 para el riesgo relativo se desarrolla así:
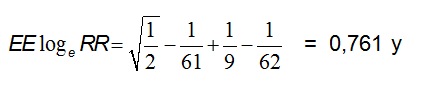
logeRR – [N0,975•EE(logeRR)] a logeRR + [N0,975 EE(logeRR)].
IC95 -1,488-(1,96•0,761) a -1,488+(1,96•0,761)
El antilogaritmo de estas cifras, recordando que e = 2,71828…, es 2,718281-2,979 a 2,7182810,00356, dando un IC95 de 0,051 a 1,003. Usando N0,95 = 1,645, el IC90 va de 0,065 a 0,789. Como el IC95 incluye a 1 en el rango, pero el IC90 no, se puede deducir que P será > 0,05 y < a 0,1. Los autores, usando el test exacto de Fisher para analizar los resultados, comunican una p = 0,02. Sin embargo, el test de Fisher de dos colas, que es el que se debió usar en el estudio, da una p de 0,053 lo que coincide con el cálculo del IC; si el cálculo se hace con una cola da una p = 0,0287. Este es el principal error en que se incurre al usar el test exacto de Fisher. Vale la pena señalar aquí que la corrección académica del autor del trabajo ha sido puesta en tela de juicio.
RAZÓN DE VENTAJAS O RAZÓN DE PROBABILIDAD (ODDS RATIO)
Los OR son de uso frecuente en tres circunstancias: para estimar la relación entre dos variables binarias, para investigar el efecto de otras variables sobre esa relación a través de la regresión logística y, para analizar el resultado de estudios de casos y controles donde no es factible usar el riesgo relativo.
Los odds, chance o posibilidad, es la probabilidad de presentar un evento comparado con la probabilidad de no presentarlo. Han recibido numerosos nombres en español como por ejemplo, entre muchos otros, razón de probabilidad, razón de chances, razón de posibilidades, razón de oportunidades, razón de productos cruzados; quizás el más curioso y que permite una digresión lingüística, y por ello vale la pena citar, es el de razón de momios, donde momio es o magro, sin gordura, o aquello que se da u obtiene sobre lo que corresponde legítimamente. La diversidad de nombres quizás refleja las dificultades en precisar y asir el concepto. Por su ubicuidad y uso común, en este artículo preferimos seguir con su denominación en inglés.
Hay una importante diferencia en la manera como se puede construir la tabla 2 x 2 en estudios retrospectivos con dos muestras. En este caso, la selección de los sujetos está basada en el resultado (las líneas) mientras que en uno prospectivo lo está en los grupos (las columnas). Debido a la manera en que se escogió la muestra no es posible analizar el riesgo de obtener un determinado resultado basándose en las características de los grupos pues se puede obtener diferentes respuestas simplemente variando el número de casos y controles. Esto hace necesario un método basado en cálculos dentro de cada grupo.
|
Factor presente (casos) |
Factor ausente (controles) |
|
| Resultado presente |
a |
b |
| Resultado ausente |
c |
d |
|
a + c |
b + d |
Como es habitual en estudios de casos y controles, el resultado de interés que define a los casos es raro por lo que a es muy pequeño y a/(a+c) será aproximadamente igual a a/c. En forma similar, b también es pequeño y b/(b+d) será aproximadamente igual a b/d. En estas circunstancias, la probabilidad del resultado de interés, de los casos de presentar el resultado comparado con los controles, es aproximadamente igual a (a/c)/(b/d) o bien ad/bc. La razón entre estas probabilidades es la razón de ventajas: el “odds ratio” (OR).
A diferencia del RR, el OR puede determinarse en cualquier tipo de estudio (transversal, prospectivo o retrospectivo). El OR es aproximadamente lo mismo que el RR cuando el evento de interés es infrecuente (< 10%). A medida que aumenta la incidencia del resultado de interés, el OR progresivamente sobrestima el RR si este es mayor de 1 o lo subestima si es inferior a 1. Si es frecuente, pueden llegar a ser bastante diferentes por lo que la recomendación es mirarlos como dos medidas independientes. Por ejemplo, para riesgo del grupo no expuesto que van de 0,001 a 0,99 y un OR 2 el RR puede ir de 1,998 a 1,005. Alternativamente, para un rango de riesgo de 0,001 a 0,5, un RR de 2 se asocia a OR que puede ir de 2,002 a infinito. En resumen, cuando un resultado es raro, la interpretación de un RR y un OR no es problema pues numéricamente son similares; sin embargo, cuando el resultado es frecuente no sucede lo mismo. Por ende un OR de 3 o de 5 no debe ser interpretado como que el riesgo se multiplica por 3 o por 5. Hay métodos para estimar el RR a partir de los OR, como el de Zang y Zu o el de Zocchetti et al. La fórmula usada por Zang y Zu es:
RR = OR/{(1-P0 )+( P 0 x OR)}
donde P0 es la proporción de individuos no expuestos (o sin el factor de riesgo) que presentan el resultado de interés. Es evidente que mientras más cerca de cero sea P 0 , el denominador se acerca a 1 y por e nde el RR se aproxima al OR. Si P 0 se acerca a 1, el RR se aproxima a 1, sin importar el valor de OR; cuando el OR se acerca a 1, el RR se acerca a 1, sin importar la P 0.
Al igual que con el RR, también se puede obtener un intervalo de confianza del OR con la siguiente fórmula (ver ejemplo):
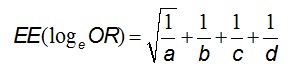
de manera que el IC95 va desde:
logeOR – [N0,975 • EE(logeOR)] a logeOR + [N0,975 • EE(logeOR)]
Cuando las muestras son pareadas, la aproximación es diferente pues se trata de mirar las diferencias entre pares cuya exposición al factor de riesgo difiere. Esto es b y c. El OR es simplemente la razón b/c.
Existen dos maneras generales de presentar los resultados en términos del RR o del OR con sus respectivos límites de confianza. Debe recalcarse que los trabajos debieran incluir estos límites, y no decir solamente si son estadísticamente significativos o no, pues ayudan a que el lector pueda interpretar la precisión de los resultados. Una manera común de expresar los límites de confianza es indicar el RR o el OR seguido, entre paréntesis, de los límites inferior y superior del intervalo de confianza en cuestión. Debe recordarse que estos límites arrojan una información similar a la de la p en términos de las probabilidades de que la hipótesis nula sea verdadera. Así, límites de confianza del 90% ó 95% pueden ser asociados con una p de 0,10 ó 0,05 respectivamente. La otra manera de presentarlos, especialmente cuando se analizan varios factores, es hacerlo gráficamente, con la estimación puntual del RR o del OR y líneas o barras horizontales que representan los intervalos de confianza respectivos y, adicionalmente, una línea vertical punteada a través del número 1. Así, cualquier intervalo de confianza que incluya esta línea vertical estará indicando que el resultado no es estadísticamente significativo con el nivel de confianza especificado (Figura 1).
EJEMPLOS DE ODDS RATIO
En un trabajo retrospectivo en pacientes consecutivos, se comparó la incidencia de reinfarto perioperatorio en 55 pacientes con un infarto previo versus 932 sin infarto previo. Dos de los 55 y 4 de los 932 presentaron un infarto para una incidencia de 3,64 vs 0,43%.
|
Infarto previo (casos) |
Sin infarto previo (controles) |
||
| Reinfarto |
2 |
4 |
6 |
| Sin reinfarto |
53 |
928 |
981 |
|
55 |
932 |
987 |
El OR calculado para esta tabla es de 8,76 y el:
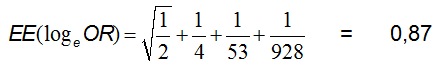
Lo que permite calcular un IC90 de 2,07 a 37 y un IC95 de 1,57 a 49. Como siempre, el intervalo menos “exigente” es más estrecho que el otro. En forma similar al ejemplo anterior, los autores, también usando un test exacto de Fisher, comunican una P < 0,05 (el cálculo con dos colas da una p de 0,039). En forma equivocada, sin embargo, por ser un trabajo retrospectivo, usan el RR anotando que el riesgo es 8,5 veces mayor (se puede calcular igual a 8,473).
En un estudio retrospectivo sobre daño ocular en el perioperatorio, se encontraron, entre otros, los siguientes resultados (Tabla 1). Aquí se apuntan cuatro factores con el objeto de resaltar el uso del OR y de los intervalos de confianza para estimar la significación estadística. Estos resultados pueden ser presentados gráficamente como se observa en la Figura 1.
Tabla 1 Factores de riesgo para daño ocular perioperatorio
|
Sin daño ocular |
Con daño ocular |
OR (IC95%) |
|
| Masculino |
23.054 |
17 |
1,6 (0,8-3,2) |
| Femenino |
37.876 |
17 |
|
| Lateral |
2.672 |
6 |
4,7 (1,93-11,3) |
| Otras |
58.259 |
28 |
|
| Cabeza y cuello |
5.937 |
11 |
4,4 (2,2-9,0) |
| Otras |
54.994 |
23 |
|
| Con intubación |
29.323 |
8 |
3,0 (1,4-6,5)??? |
| Sin intubación |
31.608 |
26 |
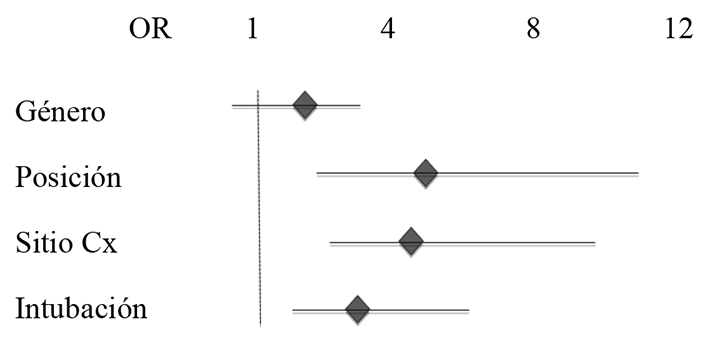
Figura 1 Razón de ventajas (OR) e IC95% de los datos contenidos en la tabla del último ejemplo.
REFERENCIAS
- Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991.
- Bland JM, Altman DG. The odds ratio. BMJ 2000; 320: 1468.
- Bland M. An Introduction to Medical Statistics, 3rd Ed, Oxford: OUP, 2006.
- Dawson-Saunders B, Trapp RG. Bioestadística Médica. México D.F: Manual Moderno, 1993.
- Holcomb WL, Chaiworapongsa T, Luke DA, Burgdorf KD. An Odd measure of Risk: Use and Misuse of the Odds Ratio. Obstet Gynecol 2001; 98: 685-688.
- Jaeschke R, et al. Basic Statistics for Clinicians: 3. Assesing the Effects of Treatment: Measures of Association. Can Med Ass J 1995; 152: 351-357.
- Kirkwood BR, Sterne JAC Medical Statistics. 2nd Ed., Oxford: Black-well, 2003.
- Morris JA, Gardner MJ. Calculating confidence intervals for relative risks (odds ratios) and standardised ratios and rates. BMJ 1988; 296: 1313-1316.
- Poldermans D, Boersma E, Bax JJ, et al. The effect of bisoprolol on perioperative mortality and myocardial infarction in high-risk patients undergoing vascular surgery. N Engl J Med 1999; 341: 1789-1794.
- Portney LG, Watkins MP. Foundations of Clinical Research. Applications to Practice. 2nd ed. Upper Saddle River: Prentice-Hall, 2000.
- Roth S, Thisted RA, Erickson JP, Black S, Schreider BD Eye injuries after nonocular surgery. A study of 60,965 anesthestics from 1988 to 1992. Anesthesiology 1996; 85: 1020-1027.
- Schechtman E. Odds Ratio, Relative Risk, Absolute Risk Reduction, and Number Needed to Treat-Which of These Should We Use? Value in Health 2002; 5: 431-436.
- Schoeppel SL, Wilkinson C, Waters J, Meyers SN. Effects of myocardial infarction on perioperative cardiac complications. Anesth Analg 1983; 62: 493-498.
- Wang Z. Converting Odds Ratio to Relative Risk in Cohort Studies with Partial Data Information. J Statistical Software 2013; 55: 1-11.
- Zhang J, Yu KF. What’s the Relative Risk? A method of correcting the odds ratio in cohort studies of common outcomes. JAMA 1998; 280: 1690-1691.
- Zocchetti C, Consonni D, Bertazzi P. Relationshio between prevalence rate ratios and odds ratios in cross-sectional studies. Int J Epidemiol 1997; 26: 220-223.
