Matías Vargas 2 , Daniela Biggs 3 , Trinidad Larraín 4 , Alexis Alvear 5 , Juan C. Pedemonte 1 ,*.
Recibido: 05-03-2022
Aceptado: 08-03-2022
©2022 El(los) Autor(es) – Esta publicación es Órgano oficial de la Sociedad de Anestesiología de Chile
Revista Chilena de Anestesia Vol. 51 Núm. 5 pp. 527-534|https://doi.org/10.25237/revchilanestv5129061230
PDF|ePub|RIS
Abstract
The emergence of artificial intelligence and machine learning in medicine determines that healthcare professionals should understand generalities of their methodologies. This narrative review consists of two parts. The first consists of an exploration of the main methods used to model in machine learning, described in a simple way by medical and mathematical authors, with the purpose to bring this methodology healthcare workers. Here we will describe the basic structure of a machine learning algorithm (input information, task to execute, output result, optimization, and adjustment), its main classifications (supervised, unsupervised and by reinforcement) and the main modeling methods used. We will review regression and then explore decision trees, support vector machines, principal component analysis, clustering, K-means, hierarchical clustering, deep learning, and convolutional neural networks. In this way, we hope to bring this methodology closer to healthcare personnel to increase the interpretability of the published work in medicine that use these methodologies.
Resumen
La irrupción de la inteligencia artificial y el amplio desarrollo de aplicaciones de machine learning que se ha experimentado en el campo de la medicina en los últimos años, requiere que los profesionales de la salud conozcan generalidades de sus metodologías. Esta revisión narrativa se compone de dos partes. La primera consta de una exploración de los principales métodos utilizados para modelar algoritmos de machine learning, descrito de manera sencilla por autores médicos y matemáticos, con el fin de acercar esta metodología a un público que se desempeña en el área de la salud. Aquí describiremos la estructura básica y los objetivos de un algoritmo de machine learning, los diferentes modelos existentes (supervisado, no supervisado y por refuerzo) y los principales métodos y técnicas estadísticas que lo componen. Revisaremos generalidades de regresiones para luego profundizar en árboles de decisiones y sus derivados, máquinas de vector de soporte, análisis de componentes principales, clustering, K-medias, clustering jerarquizado, aprendizaje profundo y redes neuronales convolucionales. De esta forma, esperamos acercar esta metodología al personal de salud con el fin de aumentar la interpretabilidad de los trabajos publicados en medicina que utilizan estas metodologías.
-
Introducción
En 1956, se utilizó por primera vez el término inteligencia artificial (IA), para referirse a la rama de las ciencias de la computación cuyo objetivo es entender y crear entidades inteligentes, usualmente como programas de software[1]. El machine learning (ML) es la capacidad de las computadoras de aprender sin ser explícitamente programadas para un determinado propósito. Esta capacidad de aprendizaje se basa en algoritmos, que son un conjunto de instrucciones definidas, no ambiguas, ordenadas y finitas. En ML, un algoritmo se aplica a los datos, lo que da origen a lo que llamamos modelo. Éstos buscan generalizar lo suficientemente bien como para predecir o clasificar casos nuevos de forma precisa. En la actualidad, es más frecuente la investigación respecto a IA sobre ML, porque los métodos de ML pueden tener en cuenta interacciones complejas para identificar patrones a partir de los datos, sin necesidad de especificar las reglas para cada tarea [2].
Modelos de Machine Learning
El ML tiene como objetivo identificar patrones a partir de los datos con el fin de hacer predicciones, detecciones o clasificaciones. Dependiendo de las características del fenómeno que se quiera analizar, se presentarán ciertas diferencias en los datos y su estructura, que harán que el algoritmo tenga que aprender de una manera determinada. Por lo anterior, los modelos de ML se pueden clasificar de acuerdo con el tipo de aprendizaje en supervisado, no supervisado y de refuerzo[3],[4].
Aprendizaje supervisado. El algoritmo aprende a partir de las variables explicativas asociadas a la variable respuesta (numérica o categórica), para predecir casos futuros a partir de datos cuya respuesta ya se conoce. Luego, predice el valor de la variable respuesta cuando se presentan nuevas variables explicativas. El proceso de análisis consiste en reunir un gran número de entradas (información inicial), con las etiquetas de salida como entrenamiento, analizando los patrones de todos los pares de entradas-salidas etiquetadas[5]. Por ejemplo, reunir una serie de síntomas de infarto al miocardio y clasificarlo como tal. Estos modelos se utilizan para identificar los parámetros óptimos que permitan minimizar la desviación entre predicción para los casos de entrenamiento y los resultados observados, con la esperanza de que la asociación identificada sea generalizable[2],[6].
Aprendizaje no supervisado. Se utiliza cuando se busca identificar patrones a partir de la similitud de sus características. El algoritmo aprende a partir de la variable explicativa sin ninguna respuesta asociada. Los algoritmos se dejan guiar por sus propios mecanismos para descubrir la estructura de datos.
El proceso de análisis infiere patrones ocultos en información no etiquetada para descubrir subgrupos, identificar datos atípicos o producir representaciones de baja dimensión de los datos, es decir, reducción del número de variables aleatorias[2],[6]. Es ideal para hacer un análisis exploratorio de asociaciones que son desconocidas previamente (descubrir patrones nuevos). Sin embargo, puede encontrar relaciones que son ilógicas desde un punto de vista del contenido del conocimiento.
Aprendizaje de refuerzo (reinforcement). En este caso el algoritmo toma decisiones usando un sistema de recompensa y castigo. El algoritmo aprende interactuando con su entorno, donde recibe recompensas por tomar la decisión ad hoc y castigos por errar. Aprende maximizando su recompensa y minimizando su penalización. Los rasgos más importantes de este método son el aprendizaje por ensayo y error asociado a la recompensa retardada[7]. Destaca por poder generar asociaciones y al mismo tiempo optimizar sus resultados.
-
Proceso de Machine Learning
Llegar a una solución analítica es un proceso que parte desde comprender el problema, estructurar y recopilar los datos para posteriormente controlar, monitorear y utilizar los resultados de la solución con el fin de calibrar el modelo (Tabla 1).
Una parte fundamental de este proceso es la etapa de entrenamiento, que corresponde al proceso donde el computador “aprende”, ya que acumula el conocimiento para luego replicarlo en otro conjunto de información. Se utilizan datos de entrenamiento para estimar los parámetros, determinar la probabilidad de clasificar a las personas o testear una regla de decisión, dependiendo de los objetivos del modelo. Para evaluar el ajuste final del modelo entrenado (valga la redundancia, por los datos de entrenamiento) se utilizan los datos de prueba[8].
| Tabla 1. Etapas del desarrollo de un modelo de Machine Learning | |
| Etapa | Explicación |
| Definición del objetivo | Establecer el objetivo del modelo a desarrollar: predecir o clasificar |
| Recopilación de datos | Recopilar los datos de los que aprenderá el algoritmo |
| Preparación de los datos | Organizar los datos en un formato apropiado, extrayendo características importantes y realizando una reducción de la dimensionalidad |
| Modelamiento | Determinar el modelo estadístico y la técnica de ML más apropiada para el problema u objeto de análisis |
| Entrenamiento | Momento en que el algoritmo de ML realmente aprende a partir de los datos que se han recopilado y preparado |
| Evaluación | Probar el modelo para identificar eficiencia y eficacia en su funcionamiento |
| Predicción | Probar el modelo con un conjunto de datos nuevos para evaluar su desempeño |
| Calibración | Controlar los resultados para ajustar el modelo con el objetivo de maximizar su rendimiento |
Los conjuntos de datos de entrenamiento y prueba son distintos. Es decir, el modelo se evalúa con un grupo de datos nuevos, para verificar si la acumulación de conocimiento generó una mejora en el desempeño (Figura 1). Usualmente, el conjunto de datos de entrenamiento es mayor que el de prueba y se obtienen de forma aleatoria. Además, habitualmente se espera que el desempeño del modelo sea peor en los datos de prueba que en los datos de entrenamiento. El entrenamiento es clave en todo proceso de ML, ya que, si se acumula información errada, el modelo va a predecir resultados incorrectos.
-
Estructura básica de un modelo de Machine Learning
La estructura de un modelo de ML puede representarse de forma simplificada. Los cuatro componentes esenciales de todo modelo de ML son:
1. Información de entrada o “input”. Constituida por los datos que le entregaremos a nuestro sistema para poder resolver la tarea.
2. Tarea para ejecutar y/o resolver. Clasificar los datos o imágenes según sus enfermedades o fenotipos.
3. Resultado de salida de la ejecución de la máquina u “out- put”. Por ejemplo, radiografías de tórax clasificadas como determinadas patologías: neumotórax, neumonía o derrame pleural.
4. Entrenamiento, optimización y ajuste. Se requiere de un proceso de entrenamiento para cada modelo y ajuste de los
resultados obtenidos en contraste con los resultados esperados, o bien, sobre el tipo de análisis efectuado.
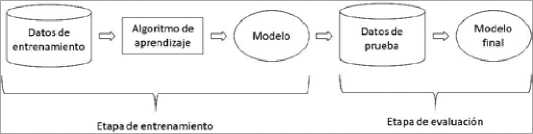
Figura 1. Proceso de entrenamiento y evaluación de un modelo de Machine Learning.
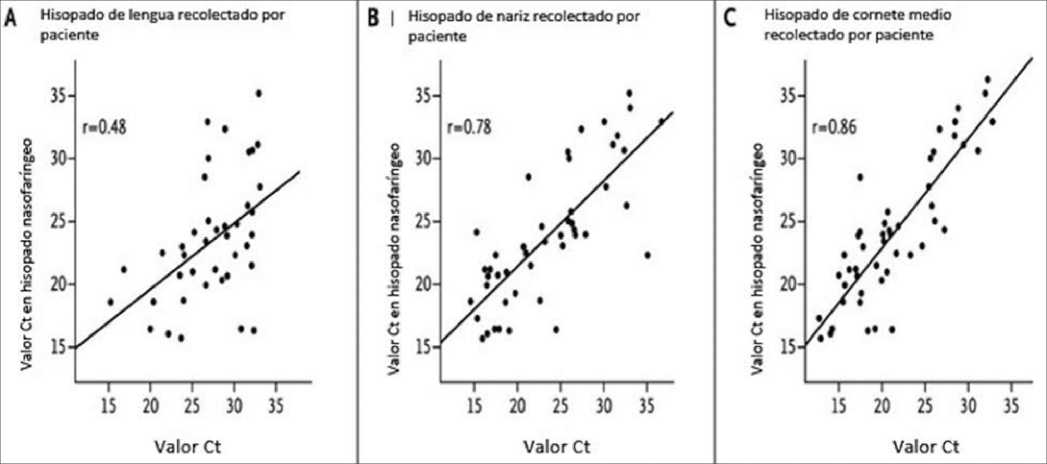
Figura 2. Ejemplo de gráficos de regresión lineal. Descripción: Se relacionan los valores del umbral de ciclo (Ct) para muestras de hisopado recogidas por pacientes en diferentes sitios, en relación con muestras de hisopado nasofaríngeo para detección de SARS-CoV-2. Modificado a partir de Tu Y-P et al. New England Journal of Medicine. 2020;383(5):494-6.
-
Estructura de modelos predictivos
Para comprender cómo funciona el ML es importante entender sus formas de metodologías predictivas:
-
I. Aprendizaje supervisado
1. Regresión lineal. Es un método estadístico para predecir una variable cuantitativa Y sobre la base de una única variable predictiva de regresión X, debido a que la relación entre ambas es lineal. Matemáticamente, se escribe Y » P0 + P1 X, siendo “»” leído como “se modela aproximadamente como…”. Los coeficientes P0 y P1 son desconocidos en la práctica, así que es necesario utilizar información o datos para estimarlos. Una vez obtenida la regresión lineal se puede evaluar la precisión de los coeficientes mediante una estimación del error. Matemáticamente, se escribe como Y = P0 + P1 X + s, donde es el error residual que no explica el modelo de regresión lineal. El uso de una variable de error residual se debe a que la verdadera relación puede no ser lineal, pueden existir otras variables que causan la variación de Y o puede existir un error de medición (Figura 2)[9].
2. Regresión lineal múltiple. Es una forma extendida de la
regresión lineal simple, útil cuando tenemos más de un predic- tor. Matemáticamente, se modela como Y = P0 + P1 X1 + P2X +…+ P n Xn + s. Conceptualmente, muestra cómo va a variar un predictor en la medida que el resto de las variables permanezcan constantes. Se utilizan, típicamente, en estudios médicos para “ajustar o corregir” por variables confundentes (siempre que la relación sea o se asuma lineal). Por ejemplo, el efecto de glucocorticoides inhalados durante la infancia (predictor que varía) sobre la altura adulta (Y) en comparación con placebo, con ajuste por variables confundentes: características demográficas, las características del asma y la estatura al inicio del ensayo[10].
3. Regresión logística. Es una forma de modelar la probabilidad de que una variable cualitativa (categórica) Y pertenezca a una categoría binaria[11]. Se utiliza la función logística, expresada como
p (X) = , e P0 + P1 X
1 + P0 + P1 X,
que entrega resultados entre 0 y 1 para cualquier valor de X y se grafica como un curva con forma de “S”, tal como se observa en la Figura 3[12]. Al igual que en la regresión lineal, los coeficientes P0 y P1 son desconocidos en la práctica y deben ser estimados con la información de entrenamiento disponible. Una de las características deseables de la regresión logística, resulta al sacar el exponente en base e del coeficiente P1, que nos permite obtener el odds ratio (OR). Esta medida es ampliamente utilizada en medicina con fin de obtener una magnitud de un efecto al comparar distintos tratamientos o intervenciones. Por esto, no nos debiese extrañar que en diversos artículos médicos es posible observar que se usa indistintamente el OR o los coeficientes P como una medida de efecto al utilizar regresión logística.
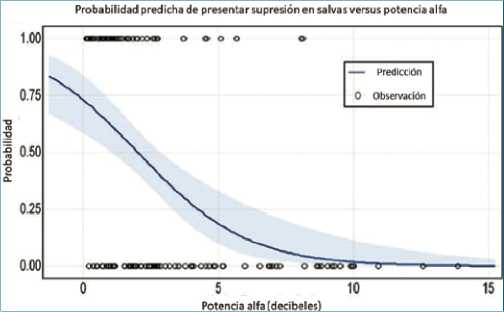
Figura 3. Ejemplo de gráfico de regresión logística. Descripción: Probabilidad predicha de presentar supresión en salvas durante el bypass cardiopulmonar (BCP) a partir de un modelo de regresión logística multivariable. Se observa la relación entre la potencia alfa en el electroencefalograma y la probabilidad de supresión en salvas durante BCP. La función física y la temperatura más baja durante la circulación extracorpórea se mantuvieron constantes en sus promedios de 46,5 puntos PROMIS y 33,2°C, respectivamente. Modificado a partir de Pedemonte JC et al. Anesthesiology. 2020;133(2):280-92.
4. Similar a lo que sucede con la regresión lineal múltiple, es posible utilizar la regresión logística múltiple si se incluye más
de una variable para predecir una variable categórica binaria. Se expresa matemáticamente como
p (X) = p (X) = , e P0 + P1 X1 + …+ PnPn
1 + eP0 + P1 X1 +…+ PnPn
y también se obtienen n coeficientes. Al sacar sus exponentes en base e nos darán n ORs que podremos utilizar para cuantificar la magnitud de efecto de una intervención. Al igual a la regresión lineal múltiple, la regresión logística múltiple nos muestra cómo va a variar un predictor en la medida que el resto de las variables permanezcan constantes. Permite “ajustar o corregir” por variables confundentes[13]. Por ejemplo, nos permite entender cómo se relacionan las exacerbaciones de la enfermedad pulmonar obstructiva crónica (EPOC) según su severidad, ajustado por otras variables como exacerbación tratada en el año anterior, historia de osteoporosis o de reflujo gastroesofágico[14].
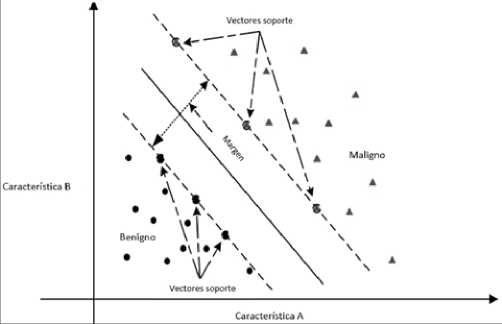
Figura 4. Ejemplo de esquema de árbol de decisión. Descripción: Representa un modelo utilizado para describir los factores asociados a la decisión de aumentar el tratamiento antihipertensivo. Modificado a partir de Verbakel et al. BMJ Open. 2015;5(8):e008657.
5. Árboles de decisiones. Consisten en una serie de reglas de división, empezando por la parte superior del árbol, para poder realizar una predicción. Los resultados finales de las divisiones son conocidos como nodos terminales u hojas del árbol, mientras que las divisiones se conocen como nodos internos. Los segmentos del árbol que conectan los nodos son considerados las ramas.
Existen dos tipos de árboles de decisión: de regresión o clasificación. El primero sirve para variables cuantitativas, mientras que el segundo para variables cualitativas. Estos pueden ser considerados por sobre los modelos lineales en casos que existe una relación no lineal y compleja entre las características y la respuesta. Son simples e interpretables, pero suelen tener menor rendimiento que otros métodos de aprendizaje supervisado, porque suelen simplificar las relaciones entre las variables que determinan una predicción (Figura 4)[15],[16],[17].
La construcción de los árboles de decisiones puede verse afectada por una alta variabilidad, es decir, se pueden obtener árboles bastante diferentes según los datos utilizados para su modelamiento. Para poder superar este inconveniente, se puede utilizar el método Bootstrap aggregation o empaquetamiento (bagging), que permite obtener un número determinado de muestras repetidas del conjunto de datos de entrenamiento
(que es único). Luego se debe entrenar el método con las muestras obtenidas y promediar las predicciones. Así, se obtiene un árbol de decisiones individual para cada muestra. Cada uno tiene una alta varianza, pero bajo sesgo. Luego se combinan todos los árboles para crear un solo árbol de decisiones, lo que reduce la varianza y aumenta la precisión del modelo predicti- vo[18].
Los bosques aleatorios (random forest) también usan Bootstrap (muestreo aleatorio con reemplazo) para obtener muestras y crear diferentes árboles. Sin embargo, se diferencian de los árboles de decisiones con empaquetamiento, ya que cada vez que se divide un árbol, se elige una muestra aleatoria de predictores como candidatos a la división del conjunto completo de predictores. La división solo puede usar uno de los predictores. Esto permite que una cantidad determinada de las divisiones no consideren al predictor más potente, para que otros predictores tengan más posibilidades de ser representados, otorgando mayor flexibilidad al modelo[16],[19].
Otra forma de mejorar los resultados de un árbol de decisiones es el impulso (boosting), donde cada árbol se ajusta a una versión modificada del conjunto de datos originales. En vez de crear todos los árboles por separado, los va creando de manera secuencial[20]. Esto significa que cada árbol se desarrolla utilizando la información de los árboles anteriores. Así, dado el árbol actual, se ajusta un árbol de decisión a los residuos del modelo actual, en vez del resultado, intentando disminuir el error residual. Luego, se añade este nuevo árbol a la función ajustada, para adecuar los residuos.
6. Máquinas de vector de soporte. En un espacio p-dimensional, un hiperplano es un subespacio plano afín de dimensión p – 1. En dos dimensiones sería una línea y en tres dimensiones, un plano. Matemáticamente, se define como P0 + P1 X1 + P2X2 + … + pnpn = 0. Si un punto X no satisface la ecuación anterior, significa que puede ser mayor o menor a 0. Esto implica que el hiperplano divide el espacio donde se distribuyen los datos en dos mitades. El hiperplano de margen máximo (maximal margin hyperplane) es aquel que se encuentra más lejos de las observaciones de entrenamiento. Podemos clasificar una observación de prueba basándonos en qué lado del hiperplano de margen máximo se encuentra, denominado clasificador de margen máximo (maximal margin classifier). Los vectores de soporte son los vectores en un espacio p-dimensional que apoyan el hiperplano de margen máximo, es decir, si se mueven estos vectores va a cambiar el hiperplano de margen máximo[21]. No puede ser utilizado en la mayoría de los datos, porque necesita que las clasificaciones sean separables por un límite y, en muchos casos, este no existe (Figura 5)[22],[ 23].
Clasificadores de vector soporte. Son una generalización del clasificador de margen máximo para casos que no son divisibles, para desarrollar un hiperplano que casi separa las clases, con un margen blando (soft margin). Esto permite una mejor clasificación en la mayoría de las observaciones y más robustez frente a observaciones individuales, a expensas de algunas observaciones clasificadas en el lado incorrecto del margen o del hiperplano[21].
Las máquinas de vector soporte son una extensión de los clasificadores de vector soporte, para acomodar límites no lineales de las clasificaciones. Se caracterizan por ampliar el es
pacio de características (feature space, dimensiones donde se encuentran las variables) de una manera específica, utilizando funciones denominadas kernels[24]. Un kernel cuantifica la similitud entre dos observaciones. Cuando el clasificador de vectores de soporte se combina con un kernel no lineal, el clasificador resultante se conoce como máquina de vectores de soporte.
-
II. Aprendizaje no supervisado
En el aprendizaje supervisado las respuestas o clasificaciones son conocidas a priori, es decir, cierta observación clasifica o no en nuestra estructura conceptual predicha. En el aprendizaje no supervisado tenemos solo las observaciones con características, sin respuestas. No sabemos qué clasificaciones o respuesta aparecerán a partir de nuestro análisis. En este caso nuestro objetivo es descubrir nueva información a partir de los datos, por lo que se suele utilizar esta aproximación para realizar un análisis exploratorio de la información[25]. Dos formas importantes son análisis de componentes principales (principal components analisys) y clustering.
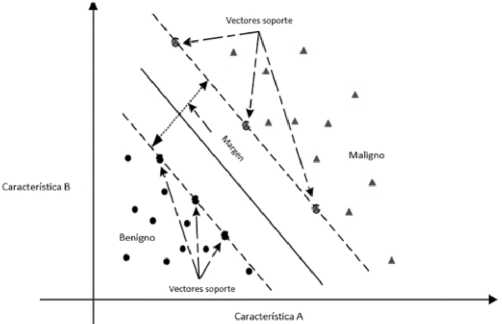
Figura 5. Ejemplo de gráfico de vector de soporte. Descripción: Se muestra un hiperplano (línea continua) y vectores de soporte (flechas de líneas intermitentes), en un espacio de características bidimensional (A y B). Las dos clases existentes son benignidad y malignidad de un cáncer. Modificado a partir de Wang H. et al. European Journal of Operational Research. 2018;267(2):687-99.
1. Análisis de componente principales. Es una técnica para reducir la dimensión de un matriz de datos[25]. Para ello, busca un pequeño número de dimensiones que sean lo más variadas posibles, siendo una combinación lineal de las características. Cuando se obtienen los componentes principales, se pueden graficar entre ellos para obtener vistas de menor dimensión de los datos (Figura 6)[26].
2. Clustering. Es un conjunto de técnicas para encontrar grupos (clusters) en un conjunto de datos, con observaciones similares dentro del grupo y diferentes con los otros. Dos métodos conocidos son K-medias (K-means) y clustering jerárquico.
a. K-medias. En este método, el algoritmo asigna cada observación a un solo grupo, luego de que se determine la cantidad de grupos deseados[27]. Los grupos obtenidos no se superponen. La idea es que cada grupo tenga la menor
variación posible, por lo que es necesario el centroide, un valor de las medias de las características de las observaciones del grupo. Posteriormente, se asigna cada observación al centroide más cercano (Figura 7)[28].
b. Clustering jerárquico. En este caso el algoritmo asigna cada observación a un grupo, determinando por sí mismo la cantidad de grupos adecuados. Se obtiene una representación similar a un árbol, denominado dendrograma. Se denomina jerarquizado porque los grupos obtenidos al cortar el dendograma a cualquier altura dada, están agrupados dentro de los grupos a mayor altura. Inicialmente, cada observación es su propio grupo. Luego, se fusionan los grupos más cercanos[29],[30]. Esto se repite hasta obtener solo un grupo final (Figura 8)[31].
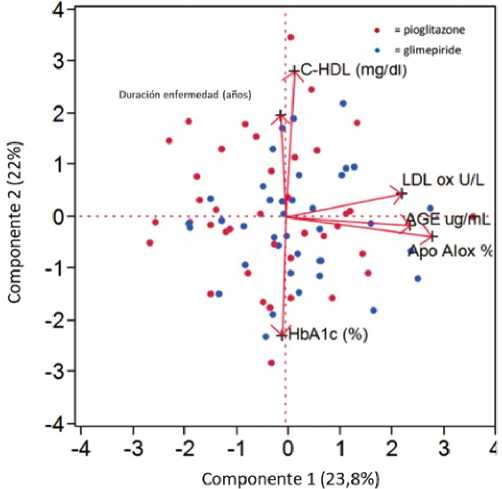
Figura 6. Ejemplo de gráfico de componentes principales. Descripción: Biplot, que incluye las puntuaciones de los componentes principales y sus cargas, de un estudio clínico respecto al efecto a largo plazo de la pioglitazona y glimepirida sobre la oxidación de las lipoproteínas en pacientes con diabetes de tipo 2. Modificado a partir de Sartore G et al. Acta Diabetologica. 2019;56(5):505-13.
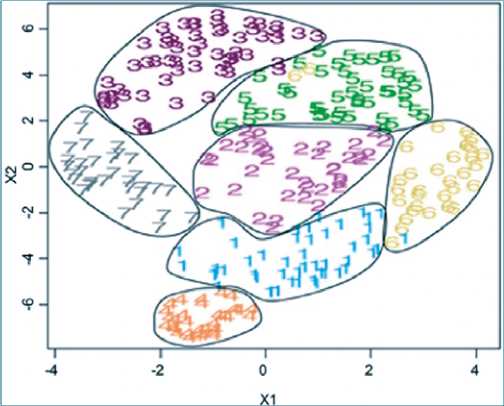
Figura 7. Ejemplo de análisis de K-medias. Descripción: Se utilizan K-medias para distinguir siete grupos fenotípicos de pacientes con lupus eritematoso sistémico. Modificado a partir de Guthridge JM. et al. EClinicalMedicine. 2020;20.
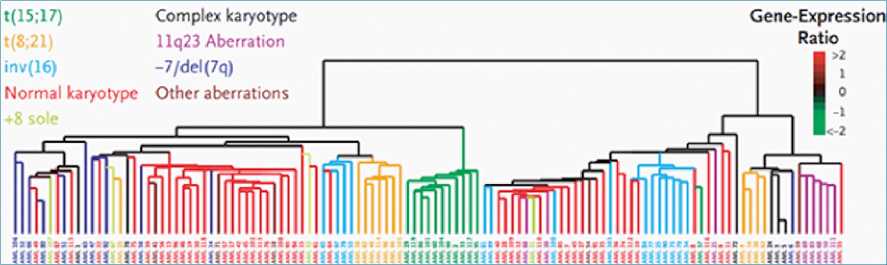
Figura 8. Ejemplo de clustering jerárquico. Descripción: En este caso se utiliza clustering jerárquico para identificar subclases pronósticas en leucemia mieloide aguda en adultos, en base a los perfiles de expresión genética. Modificado a partir de Bullinger L. et al. New England Journal of Medicine. 2004;350(16):1605-16.
3. Aprendizaje profundo (deep learning). Es un subcampo del ML que utiliza redes neuronales artificiales. Existen muchos tipos de arquitectura, según la tarea necesaria, siendo la arquitectura básica una capa de entrada y otra de salida, con un número determinado de capas escondidas entre ellas. Cada capa escondida realiza una función que integra la información de entrada y transmite el resultado a la siguiente capa, que vuelve a realizar otra función hasta que llega a la capa de salida y entrega un resultado[2],[32]. Un ejemplo de capa es conocido como convolucional, útil para extraer relaciones espaciales o temporales entre los datos (Figura 9)[33].
Los algoritmos basados en aprendizaje profundo dependen mucho de casos etiquetados, para capturar la enorme complejidad, variedad y matices propios de las imágenes[34]. Desde 2012, el aprendizaje profundo ha mostrado mejoras en las tareas de clasificación de imágenes[35], de la mano de las redes neuronales convolucionales, denominadas en inglés “convolutional neural networks” o CNN. Las CNN usan la capa convolu- cional para resumir y transformar grupos de pixeles en imágenes para extraer características de alto nivel, pudiendo operar en imágenes en bruto y aprender características útiles de los conjuntos de entrenamiento, simplificando el entrenamiento y facilitando la identificación de patrones en las imágenes[2],[36].
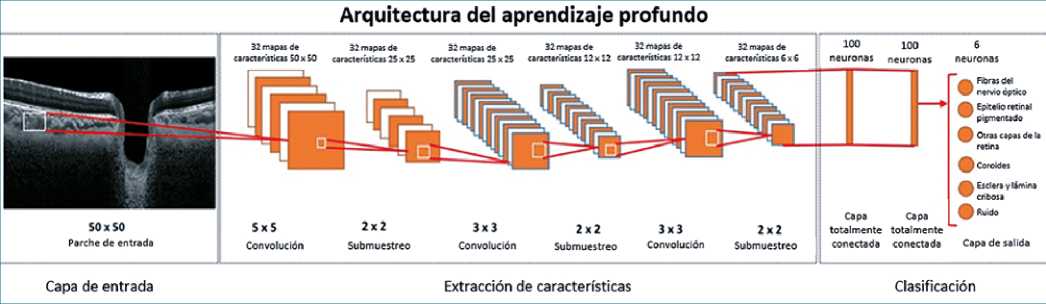
Figura 9. Arquitectura de un sistema de aprendizaje profundo. Descripción: Representación de la arquitectura de un sistema de aprendizaje profundo, diseñado para la tinción digital de imágenes de tomografía de coherencia óptica de la cabeza del nervio óptico (6). Modificado a partir de Devalla SK. et al. Investigative Ophthalmology & Visual Science. 2018;59(1):63-74.
-
Conclusiones
Los avances en la estadística han permitido que las técnicas de ML tengan un enfoque probabilístico, favoreciendo el desarrollo de herramientas para modelar y entender conjuntos de datos en estructuras complejas de forma automatizada. Por su parte, el desarrollo computacional ha permitido escalar el uso de estas técnicas estadísticas a grandes volúmenes de datos, facilitando la diversificación de sus usos y aplicaciones en diversos campos como la medicina. Los modelos de ML permiten encontrar una forma sistemática de clasificar un evento futuro (predecir) y generar nuevo conocimiento, mejorando su desempeño a medida que se acumula nueva experiencia. De este modo, genera sistemas de inteligencia artificial basados en la experiencia.
Financiamiento: Los autores no recibieron financiamiento al realizar este trabajo. Los autores declaran no posee conflictos de interés.
Referencias
1. Solomonoff R, editor. The time scale of artificial intelligence: Reflections on social effects1985.
2. Yu KH, Beam AL, Kohane IS. Artificial intelligence in healthcare. Nat Biomed Eng. 2018 Oct;2(10):719–31. https://doi.org/10.1038/s41551-018-0305-z PMID:31015651
3. Sharma D, Kumar N. A review on machine learning algorithms, tasks and applications [IJARCET]. Int J Adv Res Comput Eng Technol. 2017;6(10):1548–52.
4. Dasgupta A, Nath A. Classification of machine learning algorithms [IJIRAE]. International Journal of Innovative Research in Advanced Engineering. 2016;3(3):6–11.
5. Osisanwo F, Akinsola J, Awodele O, Hinmikaiye J, Olakanmi O, Akinjobi J. Supervised machine learning algorithms: classification and comparison [IJCTT]. Int J Comput Trends Tech. 2017;48(3):128–38. https://doi.org/10.14445/22312803/IJCTT-V48P126.
6. Deo RC. Machine Learning in Medicine. Circulation. 2015 Nov;132(20):1920–30. https://doi.org/10.1161/CIRCULATIONAHA.115.001593 PMID:26572668
7. Sutton RS. Introduction: The Challenge of Reinforcement Learning. In: Sutton RS, editor. Reinforcement Learning. Boston (MA): Springer US; 1992. pp. 1–3. https://doi.org/10.1007/978-1-4615-3618-5_1.
8. Singh A, Thakur N, Sharma A. A review of supervised machine learning algorithms. 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom). 2016:1310-5.
9. Tu YP, Jennings R, Hart B, Cangelosi GA, Wood RC, Wehber K, et al. Swabs Collected by Patients or Health Care Workers for SARS-CoV-2 Testing. N Engl J Med. 2020 Jul;383(5):494–6. https://doi.org/10.1056/NEJMc2016321 PMID:32492294
10. Kelly HW, Sternberg AL, Lescher R, Fuhlbrigge AL, Williams P, Zeiger RS, et al.; CAMP Research Group. Effect of inhaled glucocorticoids in childhood on adult height. N Engl J Med. 2012 Sep;367(10):904–12. https://doi.org/10.1056/NEJMoa1203229 PMID:22938716
11. Ray S, editor. A Quick Review of Machine Learning Algorithms. 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon); 2019 14-16 Feb. 2019. https://doi.org/10.1109/COMITCon.2019.8862451.
12. Pedemonte JC, Plummer GS, Chamadia S, Locascio JJ, Hahm E, Ethridge B, et al. Electroencephalogram Burst-suppression during Cardiopulmonary Bypass in Elderly Patients Mediates Postoperative Delirium. Anesthesiology. 2020 Aug;133(2):280–92. https://doi.org/10.1097/ALN.0000000000003328 PMID:32349072
13. Menard S. Coefficients of Determination for Multiple Logistic Regression Analysis. Am Stat. 2000;54(1):17–24.
14. Hurst JR, Vestbo J, Anzueto A, Locantore N, Müllerova H, Tal-Singer R, et al.; Evaluation of COPD Longitudinally to Identify Predictive Surrogate Endpoints (ECLIPSE) Investigators. Susceptibility to exacerbation in chronic obstructive pulmonary disease. N Engl J Med. 2010 Sep;363(12):1128–38. https://doi.org/10.1056/NEJMoa0909883 PMID:20843247
15. Muhammad I, Yan Z. Supervised Machine Learning Approaches: a survey. ICTACT Journal on Soft Computing. 2015;5(3). https://doi.org/10.21917/ijsc.2015.0133.
16. Speiser JL, Miller ME, Tooze J, Ip E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst Appl. 2019 Nov;134:93–101. https://doi.org/10.1016/j.eswa.2019.05.028 PMID:32968335
17. Verbakel JY, Lemiengre MB, De Burghgraeve T, De Sutter A, Aertgeerts B, Bullens DM, et al. Validating a decision tree for serious infection: diagnostic accuracy in acutely ill children in ambulatory care. BMJ Open. 2015 Aug;5(8):e008657. https://doi.org/10.1136/bmjopen-2015-008657 PMID:26254472
18. James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning. 112. Springer; 2013. pp. 303–35. https://doi.org/10.1007/978-1-4614-7138-7_8.
19. Dewi C, Chen RC. Random forest and support vector machine on features selection for regression analysis. Int J Innov Comput, Inf Control. 2019;15(6):2027–37.
20. Bauer E, Kohavi R. An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach Learn. 1999;36(1):105–39. https://doi.org/10.1023/A:1007515423169.
21. James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning. 112. Springer; 2013. pp. 337–72. https://doi.org/10.1007/978-1-4614-7138-7_9.
22. Alloghani M, Al-Jumeily D, Mustafina J, Hussain A, Aljaaf AJ. A Systematic Review on Supervised and Unsupervised Machine Learning Algorithms for Data Science. In: Berry MW, Mohamed A, Yap BW, editors. Supervised and Unsupervised Learning for Data Science. Cham: Springer International Publishing; 2020. pp. 3–21. https://doi.org/10.1007/978-3-030-22475-2_1.
23. Wang H, Zheng B, Yoon SW, Ko HS. A support vector machine-based ensemble algorithm for breast cancer diagnosis. Eur J Oper Res. 2018;267(2):687–99. https://doi.org/10.1016/j.ejor.2017.12.001.
24. Bzdok D, Krzywinski M, Altman N. Machine learning: supervised methods. Nat Methods. 2018 Jan;15(1):5–6. https://doi.org/10.1038/nmeth.4551 PMID:30100821
25. Mahesh B. Machine Learning Algorithms-A Review [IJSR]. Int J Sci Res. 2020;9:381–6.
26. Sartore G, Chilelli NC, Seraglia R, Ragazzi E, Marin R, Roverso M, et al. Long-term effect of pioglitazone vs glimepiride on lipoprotein oxidation in patients with type 2 diabetes: a prospective randomized study. Acta Diabetol. 2019 May;56(5):505–13. https://doi.org/10.1007/s00592-018-01278-2 PMID:30740640
27. Sinaga KP, Yang MS. Unsupervised K-means clustering algorithm. IEEE Access. 2020;8:80716–27. https://doi.org/10.1109/ACCESS.2020.2988796.
28. Guthridge JM, Lu R. Tran LT-H y cols. Adults with systemic lupus exhibit distinct molecular phenotypes in a cross-sectional study. EClinicalMedicine. 2020;20.
29. Moseley B, Wang J. Approximation bounds for hierarchical clustering: average linkage, bisecting k-means, and local search. Adv Neural Inf Process Syst. 2017;30:3094–103.
30. Bateni MH, Behnezhad S. Derakhshan M y cols, editors. Affinity clustering: Hierarchical clustering at scale. Proceedings of the 31st International Conference on Neural Information Processing Systems; 2017.
31. Bullinger L, Döhner K, Bair E, Fröhling S, Schlenk RF, Tibshirani R, et al. Use of gene-expression profiling to identify prognostic subclasses in adult acute myeloid leukemia. N Engl J Med. 2004 Apr;350(16):1605–16. https://doi.org/10.1056/NEJMoa031046 PMID:15084693
32. Li Y. Deep reinforcement learning: An overview. arXiv preprint arXiv:170107274. 2017.
33. Devalla SK, Chin KS, Mari JM, Tun TA, Strouthidis NG, Aung T, et al. A Deep Learning Approach to Digitally Stain Optical Coherence Tomography Images of the Optic Nerve Head. Invest Ophthalmol Vis Sci. 2018 Jan;59(1):63–74. https://doi.org/10.1167/iovs.17-22617 PMID:29313052
34. Beam AL, Kohane IS. Big Data and Machine Learning in Health Care. JAMA. 2018 Apr;319(13):1317–8. https://doi.org/10.1001/jama.2017.18391 PMID:29532063
35. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems – Volume 1; Lake Tahoe, Nevada: Curran Associates Inc.; 2012. p. 1097–105.
36. Albawi S, Mohammed TA, Al-Zawi S, editors. Understanding of a convolutional neural network. 2017 International Conference on Engineering and Technology (ICET); 2017 21-23 Aug. 2017. https://doi.org/10.1109/ICEngTechnol.2017.8308186.

 ORCID
ORCID