Aurio Fajardo Campoverdi MD. MSc. 1 ,a,*, Rodrigo Adasme Jeria 2 ,3,a, Michael Maturana Quiñones 3 , Angelo Roncalli Rocha PT. MSc. 4 ,a, William Cristancho Gómez 5 ,a
Recibido: 12-10-2021
Aceptado: 15-11-2021
©2022 El(los) Autor(es) – Esta publicación es Órgano oficial de la Sociedad de Anestesiología de Chile
Revista Chilena de Anestesia Vol. 51 Núm. 2 pp. 173-183|https://doi.org/10.25237/revchilanestv5104021724
PDF|ePub|RIS
High-flow oxygen therapy masks: Are they really Venturi?
Abstract
Oxygen therapy is the mainstay for the treatment of hypoxia. The use of devices capable of satisfying the necessary flow demanded by the patient also offers stable and predictable oxygen concentrations, which is why they are currently considered a reliable and safe therapeutic tool. The physical mechanism for the operation of these devices is based on a modification of Bernoulli’s principle. The supply of a constant flow of oxygen, when its pressure drops, increases its velocity and consequently allows the incorporation of ambient air into the system. However, in order to be granted the Venturi designation, structural requirements in geometrical, physical and thermodynamic terms must be met. The ISO standard specifies a Venturi tube by three fundamental parts: a contraction zone (inlet of a continuous flow of a gas), a constriction zone (smaller in radius than the con- traction zone, so as to increase the fluid velocity) and a diffusion zone (outlet of a gas mixture with ambient air). In conclusion, the designation of Venturi to high-flow oxygen therapy masks is at least questionable.
Resumen
La oxigenoterapia es el pilar fundamental para el tratamiento de una hipoxia. El empleo de dispositivos capaces de satisfacer el flujo necesario demandado por el paciente ofrece además concentraciones estables y predecibles de oxígeno, por lo que actualmente son considerados una herramienta terapéutica fiable y segura. El mecanismo físico para el funcionamiento de estos dispositivos se basa en una modificación del principio de Bernoulli. El aporte de un flujo constante de oxígeno, al sufrir una caída de su presión, aumenta su velocidad y como consecuencia permite la incorporación de aire ambiental en el sistema. Sin embargo, para otorgarse la denominación de Venturi, deben cumplirse requisitos estructurales en términos geométricos, físicos y termo- dinámicos. La norma ISO especifica a un tubo Venturi mediante tres partes fundamentales: una zona de contracción (entrada de flujo continuo de un gas), una zona de constricción (de menor radio que la zona de contracción, de tal manera que permita aumentar la velocidad del fluido) y una zona de difusión (salida de una mezcla de gas con aire ambiental). En conclusión, es al menos cuestionable, la denominación de Venturi a las mascarillas de oxigenoterapia de alto flujo.
La oxigenoterapia se define como el aporte extra de oxígeno inspirado sobre la concentración ambiental, cuyo objetivo principal es disminuir el trabajo respiratorio y miocárdico a través de la corrección de la hipoxemia (aguda o crónica), debido a la mejora en la oferta tisular. Se define como hipoxemia a la situación en la cual la presión arterial de oxígeno (PaO2) es menor a 60 mmHg, lo que teóricamente corresponde a una saturación periférica (SpO2) de 90%[1], a una fracción inspirada de oxígeno ambiental (FiO2 21%).
El oxígeno (O2) se transporta principalmente unido a la hemoglobina en hasta 97% y el resto lo hace disuelto en el plasma y a nivel celular. Cada gramo de hemoglobina puede liberar hasta 1,3 ml de O2, por lo tanto, la hemoglobina de 100 ml de sangre se puede combinar con hasta 20 ml de O2 cuando la hemoglobina está saturada 100%. Existen varios factores que desplazan la curva de disociación de la hemoglobina, alterando su capacidad de fijación y transporte de O2 (Efecto Bohr; Figura 1). En este sentido, cuando la presión parcial de oxígeno se eleva, favorece la unión de O2 a la hemoglobina y además la liberación de dióxido de carbono (Efecto Christiansen-Douglas- Haldane). De esta forma, cuando la PaO2 es menor a 60 mmHg, la afinidad de la hemoglobina por el O2 disminuye y en consecuencia existe hipoxia. La corrección de este trastorno es fundamental para mantener la homeostasia tisular[1].
Sin embargo, existen otras causas de hipoxemia explicadas mediante los siguientes mecanismos conocidos:
1. Por disminución de la presión de O2 del aire inspirado (PiO2), baja presión atmosférica, por desplazamiento del O2 en el aire (Dishemoglobinemias) o por respirar gases tóxicos.
2. Hipoventilación alveolar, como en la alteración del centro respiratorio o en la falla respiratoria tipo 2.
3. Alteración en la difusión a nivel de la membrana alveolo-capilar.
4. Alteración de la relación ventilación – perfusión (V/Q).
5. Aumento del cortocircuito intrapulmonar (“shunt”).
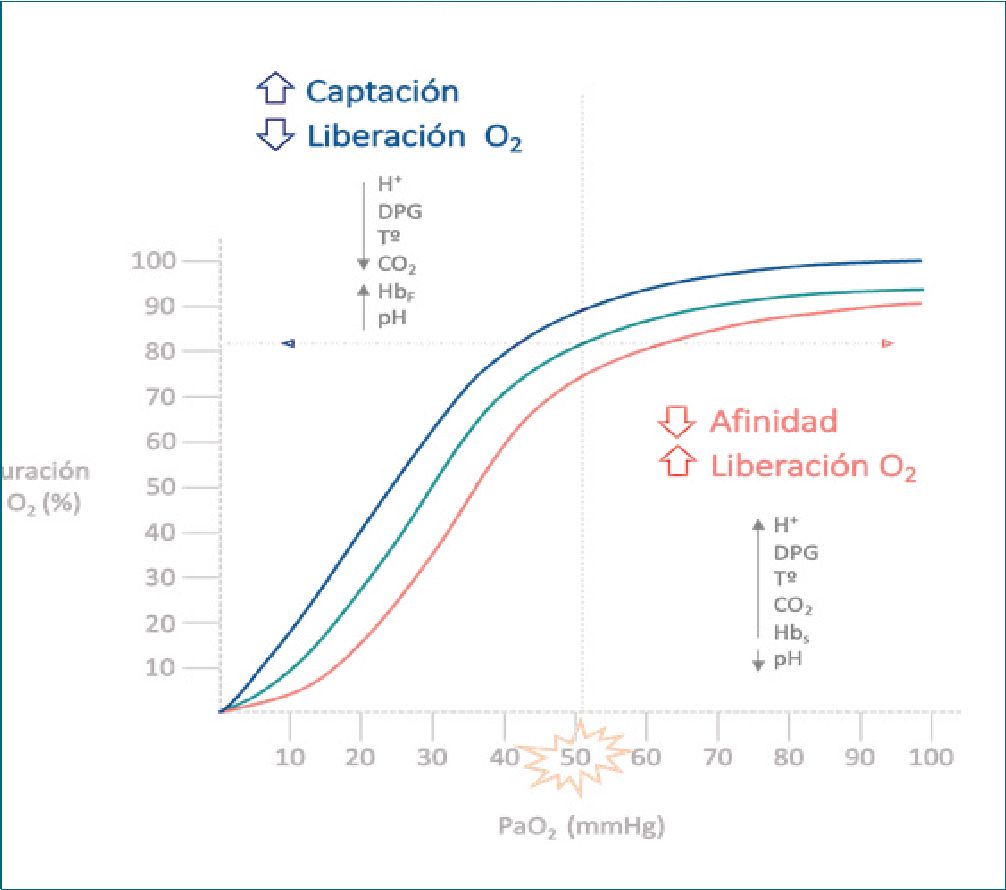
Figura 1. Curva de disociación de la hemoglobina. Representación del porcentaje de saturación de O2 de la hemoglobina en función de la presión parcial de O2: a medida que aumenta la PaO2 sanguínea hay un aumento progresivo del porcentaje de hemoglobina con O2.
Tras el inicio de la hipoxemia, se activan diferentes mecanismos de compensación en un intento por corregir el defecto de aporte de O2. Sin embargo, dichos intentos de compensación podrían terminar en un aumento del trabajo respiratorio y en un progresivo agotamiento ventilatorio. Por otro lado, aumentará el estrés miocárdico y en consecuencia aumentará el consumo de O2 a ese nivel. Estos mecanismos compensatorios son:
1. Ventilatorio: Incremento de la ventilación alveolar a expensas del volumen minuto
2.Cardiovascular: Incremento del gasto cardiaco mediante el aumento de la frecuencia cardíaca
3.Hematológico: Poliglobulia (en cronicidad o adaptación a alturas)
4.Metabólico: Ante acidemia, mediante activación del eje renina-angiotensina-aldosterona
Ante una hipoxia, la microcirculación pulmonar experimenta un fenómeno adaptativo y exclusivo de vasoconstricción, con el objetivo de redistribuir transitoriamente el flujo sanguíneo desde zonas pobremente aireadas hacia las que mejor lo están, disminuyendo así el shunt intrapulmonar y logrando optimizar la oxigenación. El equilibrio ventilación/perfusión (V/Q) es el factor fundamental para optimizar el intercambio gaseoso. En condiciones de normoxia, el ratio V/Q es igual a 1 con aproximadamente 5 L/min de flujo vascular. El reflejo de vasoconstricción pulmonar hipóxico(VPH)[1] disminuye el flujo vascular (Q) de las áreas pulmonares donde la presión alveolar de oxígeno (PAO2) es baja (V/Q bajo) y lo redistribuye hacia las zonas con mejor ventilación (V).
Al enriquecer el O2 inspirado, se aumenta la PiO2 y con ello teóricamente se revierten la hiperventilación (por aumento de la oferta), el trabajo respiratorio y el trabajo cardiaco. El resultado final será la corrección de la hipoxia tisular[1], atenuando el estrés mitocondrial. Sin embargo, una vez que se corrige la hipoxia (cesa el reflejo de vasoconstricción pulmonar) y se mantiene el aporte adicional de FiO2, podrían ocurrir desequilibrios a nivel de la relación V/Q por alteración de la PAO2.
En pacientes críticamente enfermos en los que prevalece la hipoxemia, el uso de oxígeno suplementario deberá hacerse con mucha cautela, fijando un objetivo de saturación acorde a la patología actual y remota del paciente, así como también limitando su uso según el tiempo necesario de tratamiento. La evidencia actual sugiere que la hiperoxia se relaciona con peores desenlaces[2]. Por este motivo, es importante recordar que el O2 es un medicamento que deberá ser aportado bajo estricta prescripción y vigilancia.
El objetivo principal será suplir la demanda inspiratoria de forma individualizada, ya sea de flujo o de una combinación de flujo con O2. Se conocen algunas situaciones puntuales a corregir:
– Hipoxemia arterial: donde juega un rol imprescindible el desequilibrio V/Q.
– Hipoventilación alveolar: que puede ser central o periférica.
Importante dilucidar entre requerimiento de oxigenoterapia vs soporte ventilatorio.
– Shunt derecha-izquierda: se considera “normal” hasta un 20% en el adulto[1] objetivable mediante ecocardiografía. Cuando existen patologías cardiogénicas cianotizantes, la hipoxemia persiste pese a la oxigenoterapia.
– Grandes alturas: hipoxemia a causa de la disminución de la presión parcial de oxígeno ambiental.
– Hipoxia tisular sin hipoxemia: deterioro de la oferta tisular
– Bajo débito.
– Intoxicación por monóxido de carbono.
Indudablemente el primer objetivo será lograr una PaO2 mayor a 60 mmHg o SpO2 igual o mayor a 90%, si se cumplen las condiciones adecuadas de perfusión distal.
Aquellas personas que cursen con una insuficiencia respiratoria aguda, presentarán aumento del trabajo respiratorio (taquipnea, disnea, hiperpnea). En este punto, se requiere un aporte de O2 con flujos variables para lograr compensar la demanda inspiratoria del paciente.
Se recomienda fijar un objetivo de SpO2 de entre 88% a 92% en falla tipo 2 (hipoxémica e hipercápnica), ya que el aporte de un flujo inapropiado o insistir en conseguir una SpO2 elevada en estos pacientes, será definitivamente deletéreo y aumentará la morbimortalidad[3]. La hiperoxia induce una compleja respuesta endotelial, epitelial, plaquetaria e inmune a nivel alveolar. Histológicamente, conduce a una destrucción progresiva de la membrana alveolo-capilar lo cual produce un aumento del espacio muerto, hemorragia alveolar[4] y remodelación de la red vascular con predisposición a la formación de microtrombos[5]. Además, hay pérdida de la funcionalidad de los microcapilares, provocando congestión y aumento de la presión transcapilar, lo cual finalmente predispone al desarrollo de hipertensión pulmonar[6].
Es importante definir a los dispositivos clasificados como de alto y bajo flujo de acuerdo con las características propias del dispositivo; lo cual, en condiciones reales dependerá del flujo inspiratorio de cada sujeto y de la capacidad del dispositivo para suplir dicha demanda. Son dispositivos de alto flujo aquellos en los que el flujo aportado supera la demanda inspiratoria del paciente, y por lo tanto, el gas inspirado proviene en su totalidad desde el dispositivo. Por otro lado, son dispositivos de bajo flujo cuando parte del gas inspirado proviene del ambiente y del dispositivo, y por lo tanto, proveen concentraciones de oxígeno poco estables.
El aporte de flujos elevados permite brindar mezclas de gas con FiO2 a concentraciones mas precisas, para satisfacer la demanda inspiratoria del paciente. La FiO2 aportada dependerá del diseño del dispositivo (o mascarilla en este caso), pero también del flujo y del tipo de gas aportado. El mecanismo de acción dependerá entonces del principio mediante el cual se incorpora la entrada de aire, lo que ocurrirá como consecuencia de la viscosidad del fluido (gas). Las mascarillas Ventimask® o Multivent® disponen de un mecanismo de funcionamiento que ofrece una FiO2 mixta cuyo ajuste estará supeditado al tipo de inyector, que puede ser una ventana regulable o un código de flujo y FiO2. Su accesorio blanco por ejemplo (Figura 2), proporciona una FiO2 teórica máxima del 50% y el accesorio verde entrega una FiO2 que va desde 24% hasta 40%. Además, existe variabilidad comercial entre países. Otros tipos de mascarillas presentan variadas piezas para diferentes tipos de concentración de oxígeno, lo cual los vuelve poco prácticos.
Las mascarillas similares a Ventimask® o Multivent® (como dispositivos de alto flujo) funcionan bajo el principio de Bernoulli; sin embargo, no cumplen las características estructurales de un tubo Venturi.
-
Principio de Bernoulli
Para entender objetivamente lo que implica un sistema Venturi, el punto de partida es comprender de que se trata el efecto Bernoulli[7].
Basado en la ley de Boyle que rige a los gases (gases ideales y en espacios cerrados), y principalmente basado en la primera ley de la termodinámica o ley de la conservación de la energía: cuando existe un descenso de la presión de un sistema debido a un estrechamiento en la vía del flujo continuo de alta velocidad, se incrementa la energía cinética a expensas de la energía de presión[8]. En otras palabras, el Efecto Bernoulli no es más que la disminución de la presión al aumentar la velocidad del flujo constante de un fluido, en este caso oxígeno (y posteriormente una mezcla con aire ambiental).

Figura 2. Accesorios de mascarilla Multivent® para regulación del flujo y FiO2: A) Aporte de FiO2 bajas, B) Aporte de FiO2 intermedias, C) Diferentes aportes de FiO2.
La energía cinética por unidad de volumen es la sumato- ria de toda la energía implicada en el movimiento del flujo de cualquier fluido. Cuando existe flujo turbulento o movimiento caótico, significa entonces que la energía cinética no está contribuyendo del todo al avance del fluido.
En la Figura 3A; basado en la ecuación de Bernoulli se interpreta que la presión 2 (P2), una vez que el flujo supera el estrechamiento, volvería al valor de presión 1 (P1) ya que el radio final (A2) vuelve a tener un valor similar al radio original (A1). Sin embargo, esto no es tan así y se debe en parte a la pérdida de la energía del flujo por la fricción ocasionada a consecuencia del movimiento molecular desordenado, aunque algunos autores creen que esta disipación viscosa es despreciable.
Considerando que el aire tiene un comportamiento dinámico que lo define como fluido newtoniano (su viscosidad es independiente del gradiente de velocidad y puede depender solo de la temperatura y quizá de la presión), habrá que estimar además las pérdidas por fricción (despreciable). La Ley de Poiseuille[9], teóricamente modela un flujo laminar cuyo avance depende además de la viscosidad del fluido, y por ende resultará en una disminución de la presión a medida que avanza dicho fluido. La Ley de Poiseuille postula que el caudal del volumen está determinado por la diferencia de presión, partida por la resistencia que ofrece linealmente la viscosidad, la longitud y la cuarta potencia del radio.
Se conoce como “flow rate” al volumen de fluido por unidad de tiempo, el cual será constante en cada punto a lo largo del tubo contenedor del flujo. El “flow rate” se calcula al multiplicar el área transversa por la velocidad del flujo (distancia recorrida por unidad de tiempo) y se mide en m3/segundo. Por lo tanto, la velocidad del fluido a nivel de la constricción del tubo deberá incrementarse a medida que disminuye el área transversa, para así conservar un caudal constante[10].
Otro concepto importante a considerar, es el número de Reynolds (Re)[7]. Es un número adimensional, cuya aplicación predice el patrón de flujo de un fluido en una tubería. Expresa la relación entre las fuerzas de inercia y las viscosas de un fluido, siendo la fuerza de inercia el producto de la velocidad promedio y del diámetro interno, y siendo la fuerza viscosa la viscosidad cinemática.
El punto de corte para diferenciar un fluido laminar de uno turbulento, son Re 2.000 (número de Reynolds crítico inferior). Por consiguiente, si aplicamos este concepto al principio de Ber- noulli (Figura 3A), queda claro que la velocidad del flujo es mayor en el centro del tubo y en consecuencia se torna turbulento o inestable, lo cual estaría representado por un Re mayor a 2.000. Por definición, un fluido que circula en régimen laminar cumple con la Ley de Newton de la viscosidad. Si aplicamos este concepto a una conducción cilíndrica, el resultado de incluir la Ley de Newton de la viscosidad en un sistema que incluya la ecuación del movimiento y la ecuación de la continuidad, da como resultado que el fluido tenga un perfil parabólico de velocidades (Figura 4), siendo máxima en el centro y cero en las paredes de conducción (por fricción). De esta manera, las “láminas” del fluido en movimiento permanecen bien definidas viajando cada una a su velocidad, sin mezclarse (régimen ordenado).
Existe un régimen de “transición” que implica un Re entre 2.100 y 4.000, en el cual se da el paso cíclico de flujo laminar hacia turbulento, y predominan las altas vibraciones y diferentes pérdidas de carga.
Finalmente, si el Re es mayor a 4.000, la Ley de Newton de la viscosidad se pierde, convirtiendo prácticamente en imposible la analítica del perfil de velocidades. Este régimen turbulento se caracteriza por un movimiento caótico de las partículas, formando incluso remolinos aperiódicos. El motivo por el cual se produce la transición de régimen laminar a turbulento tras un incremento del caudal, es aún desconocido.
En estricto rigor, el principio de Bernoulli no es aplicable a un flujo turbulento (pero tampoco a un flujo laminar), a menos que se añadan las pérdidas de carga primarias y secundarias; es decir, se compensen las perdidas por fricción. De todas maneras, este concepto rige como un aproximado para explicar el funcionamiento de los sistemas de inyección de un fluido.
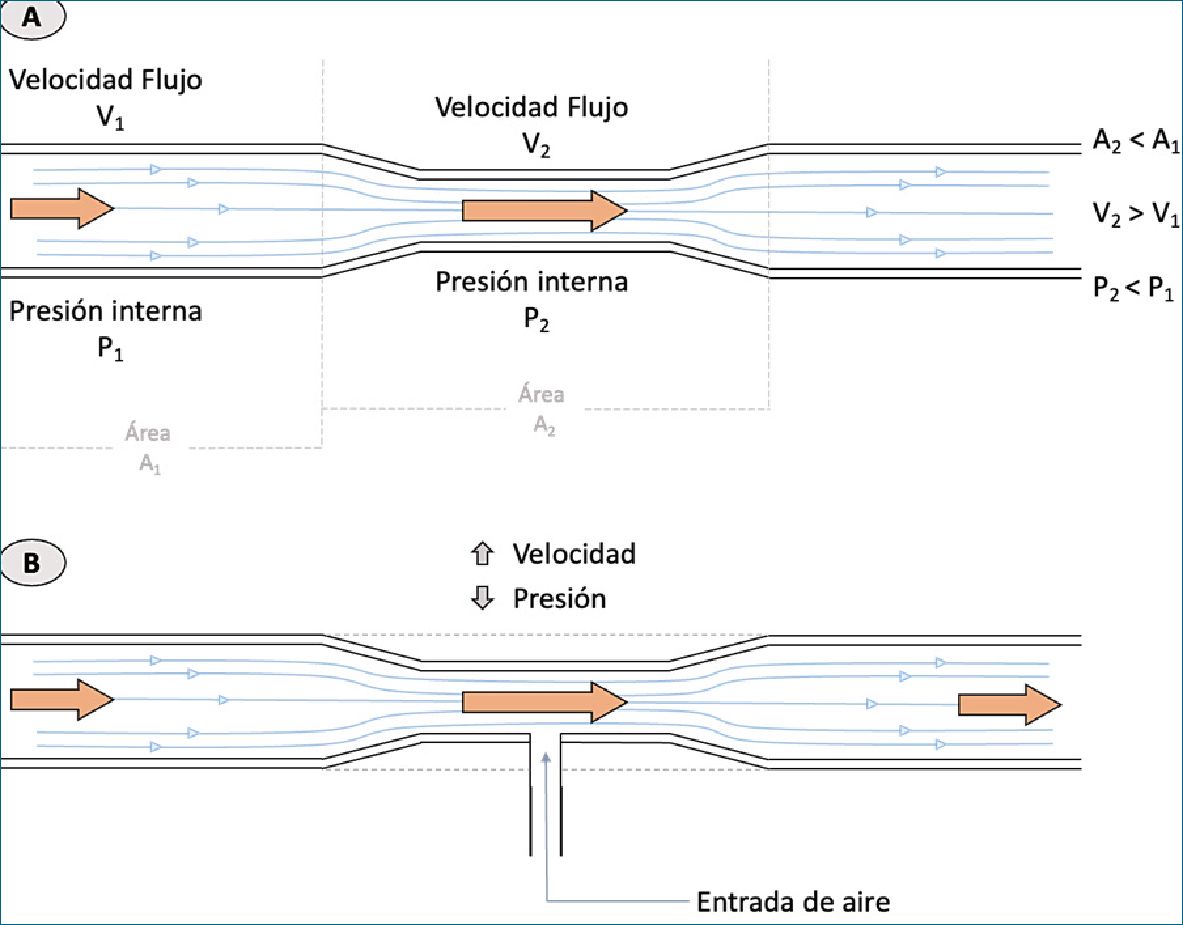
Figura 3. A) Representación del principio de Bernoulli, B) Representación del efecto Venturi.
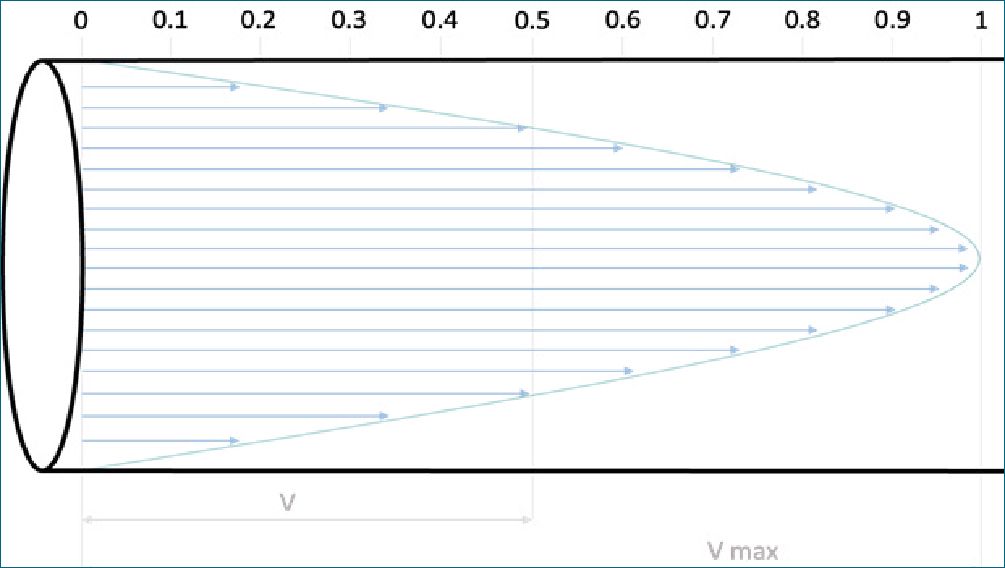
Figura 4. Perfil de velocidades en régimen laminar: V = velocidad, Vmax = velocidad máxima. Nótese que la velocidad es cero en la pared de conducción y máxima en el centro, e igual al doble de la velocidad media.
El diseño de este sistema fue descrito en 1797 por Giovan- ni Battista Venturi, el cual aplica el principio de Bernoulli para un gas que fluye a través de un tubo con un estrechamiento (constricción) y aprovecha la caída de la presión interna para incorporar, a manera de mezcla, otro gas (Figura 3B). En otras palabras, las moléculas del gas son aceleradas al entrar en la zona de constricción debido a la caída de la presión en ese nivel; sin embargo, tras superar la constricción el gas volverá a ser sometido a presiones altas post constricción y por tanto, se enlentecerá el movimiento molecular del gas (Figura 3A).
Un inyector es un dispositivo que, al aplicar el principio de Venturi, bombea un fluido a alta velocidad a través de una boquilla hacia una zona de baja presión, logrando mezclar dos fluidos y otorgándole velocidad final.
El movimiento molecular a nivel de la constricción viaja de una manera menos caótica, y en consecuencia existe menor fricción contra las paredes del tubo, disminuyendo la frecuencia e intensidad de la fuerza con la que lo hace. En este punto, es importante entender que las moléculas del aire están siempre en constante movimiento “salvaje” o de rebote, lo cual ocasiona que incluso choquen entre si a altas velocidades. La velocidad promedio de una molécula de aire, a temperatura ambiente, es de alrededor de 500 m/s y se denomina “velocidad térmica”. A medida que las moléculas del gas se acercan a la constricción del tubo Venturi, las que tienen mayor probabilidad de entrar en dicha constricción son aquellas cuyo mayor movimiento térmico ocurre en dirección del flujo y aquellas con un mínimo componente perpendicular (fricción). Por consiguiente, esas moléculas viajan más rápido a través de la constricción usando parte de su velocidad térmica. El resto de las moléculas seguirán el mismo patrón una vez que haya cesado su característico movimiento de rebote y logren alinearse en dirección del flujo. En suma, la constricción actúa como un filtro de velocidad al seleccionar las moléculas cuyas velocidades térmicas logran alinearse a lo largo de la dirección del flujo, aumentado entonces la velocidad de dicho flujo y disminuyendo la probabilidad de colisión contra las paredes[11]. Una vez que las moléculas abandonan la zona de constricción, retoman su típico movimiento caótico multidireccional, el cual determina el enlentecimiento de la velocidad del flujo del gas.
Con respecto al flujo de descarga (post tubo), es decir al momento de la transición tubo-mascarilla, una interesante aproximación podría ser explicada mediante la utilización del principio de Torricelli; el cual, siendo una aplicación del principio de Bernoulli, explica el caudal de salida del flujo a través de un orificio como consecuencia de la interacción entre las fuerzas dentro de su contenedor (viscosidad, tensión superficial) y la fuerza gravitacional[12], acelerando las partículas en la zona de restricción para mantener la estabilidad del sistema.
Cien años después de la descripción del tubo Venturi, se atribuye a Earl Moran Campbell[13] su aplicabilidad (teórica) en la medicina mediante la creación de oxigenoterapia con altas concentraciones de O2 proporcionadas a través de una máscara facial. Moran Campbell encontró la forma de aportar oxigeno- terapia, y al mismo tiempo prevenir la retención de CO2, al usar O2 combinado con aire ambiental. En condiciones basales, el lavado de CO2 se asegura con un flujo continuo de al menos 30 litros por minuto[14], y aumentará en función del espacio muerto del dispositivo utilizado. Por otro lado, el uso de FiO2 altas está directamente relacionado con atelectasias por reab- sorción[15].
Teóricamente, se describe por primera vez[16] una máscara facial que ofrece O2 al 100% y que al utilizar un sistema Venturi crea una presión negativa que le otorga un efecto de succión que incorpora aire ambiental, el cual se mezcla con el flujo inicial de O2 aportando concentraciones controlables y predecibles de FiO2. Entonces, se definió como máscara facial Venturi aquella que recibe un flujo específico y constante de O2, el cual circula a través de un tubo cuya estructura cuenta con una zona de constricción. Además, este circuito cuenta con un orificio lateral que, al caer la presión en la zona de constricción, crea un efecto de succión y en consecuencia incorpora aire ambiental al circuito (inyectores). La primera máscara facial creada por Moran Campbell entregaba una concentración de O2 de 0,24; 0,27 y 0,35 el cual era determinado por el ancho del “jet” (tamaño de la apertura que acelera la velocidad del flujo) dentro del sistema[16]. Con el paso del tiempo, esta mascarilla ha ido evolucionando. Actualmente, es capaz de entregar concentraciones de O2 entre 0,24 a 0,60(17); e incluso, los orificios laterales pueden variar en tamaño dependiendo de la cantidad de O2 a entregar[18]. Por lo tanto, el flujo final y la FiO2 a entregar, dependerá directamente del tamaño de la restricción y del tamaño de la ventana (orificios laterales), permitiendo incluso un cálculo exacto de FiO2.
No obstante, es totalmente válido cuestionar si acaso el soporte con oxigenoterapia que usa un sistema de mezcla tipo “jet”, efectivamente cumple las condiciones físicas necesarias para generar el efecto Bernoulli. Este cuestionamiento fue planteado por Scacci en 1979[19], quien además detalló 3 fundamentos para diferenciarlos:
1. El principio de Bernoulli produce entrada de aire ambiental en su sistema.
2. El aire entra al sistema de flujos debido a la diferencia de presiones, inducida por el flujo primario del gas.
3. Un aumento del flujo primario de oxígeno incrementará la concentración de oxígeno entregada.
Desde una perspectiva física y aplicando los conceptos de la dinámica de fluidos, aquellas máscaras de oxigenoterapia que usan un sistema de flujo tipo “jet” (Multivent® o VentiMask®) lo hacen mediante la aplicación de una presión constante que genera una fuerza necesaria (trabajo) para movilizar una masa estática de gas (aire ambiental)[20]. En suma; en este sistema tipo “jet” la entrada de aire ocurre como una consecuencia de la viscosidad del fluido (gas), el cual genera fuerzas de cizalla- miento entre las capas estáticas y dinámicas de dicho fluido, causando que el gas estático sea arrastrado dentro de la masa en movimiento[21]. Cualquier gradiente de presión que se genere, será consecuencia del proceso de mezcla. Finalmente, la concentración de O2 necesariamente se verá afectada por cambios en el flujo primario.
Según la Norma ISO 5167-4, se define como tubo Venturi a todo dispositivo compuesto de un cilindro de entrada, una sección convergente conectada a un cuello cilíndrico y éste a su vez está conectado a una sección cónica divergente. Ningún diámetro, a lo largo del cilindro de entrada (contracción), debe diferenciarse en mas de 0,4% del valor del diámetro medio. La sección convergente debe ser cónica y debe tener un ángulo comprendido entre los lados de 21° ± 1° (Figura 5). Además, su superficie interna debe ser libre de grietas, fisuras o irregularidades. Ningún diámetro, a lo largo del cuello (restricción), debe diferenciarse en más de 0,1% del valor del diámetro medio. La sección divergente debe ser cónica y puede tener un ángulo comprendido entre los lados de entre 7° y 15°. Sin embargo, su diámetro más pequeño no debe ser menor que el diámetro del cuello. De todas maneras, la Norma ISO 5167 se aplica solo a tubos Venturi en los que el flujo permanece subsónico en toda la sección medida, y donde el fluido puede considerarse monofásico.
Se conoce como coeficiente de descarga (C) al factor adimensional propio de una válvula, que permite el cálculo del caudal con el que se desembalsa una válvula en función del nivel del fluido en el embalse. Tiene un valor prácticamente constante para cualquier diámetro de un mismo modelo. A mayor valor del coeficiente de descarga (a una misma diferencia de altura del embalse) mayor caudal y por tanto más rápido podrá desembalsarse determinado depósito, a través de la válvula. Para un tubo Venturi clásico, según Norma ISO 5167, el valor de C = 0,095.
La Norma ISO 3534-1:1993, define como incertidumbre a una estimación unida al resultado de un ensayo que caracteriza el intervalo de valores dentro de los cuales se afirma que está el valor verdadero. Este valor es desconocido. En relación con la ingeniería de materiales, la incertidumbre relativa del C es igual a 1%.
Cuando el Re disminuye por debajo de 2 x 105, se encuentra con frecuencia que hay un pequeño aumento del coeficiente de descarga, antes de haber una disminución constante con Re decreciente. La incertidumbre de C se incrementa despacio en principio, pero después lo hace rápidamente. Cuando Re aumenta por encima de 106, la pauta de C, en función del número de Reynolds, no es previsible. Hay evidencia suficiente para afirmar que el coeficiente de descarga de un tubo Venturi va en función de Re basado en el diámetro del cuello.
Simplificando, un tubo Venturi está compuesto por una sección transversa que se contrae gradualmente (contracción), una zona de transición (constricción) y una zona de difusión (Figura 5). Cuando un fluido recorre la zona de transición, el estrechamiento acelerará dicho fluido debido a una caída de la presión.
Se han propuesto modificaciones estructurales de este modelo, para lograr controlar tanto la velocidad como la caída de la presión del fluido en el tubo. En este contexto, algunos autores han modificado el ángulo de difusión para así lograr mayor masa de flujo[22], otros modificaron la válvula de entrada de aire[23], otros modificaron el flujo a bifásico[24] y últimamente se ha estudiado el resultado de modificar en conjunto el radio de contracción (entrada), el ángulo de difusión y el grado de succión[25]. Para obtener un incremento en el delta de presión entre la masa de flujo de entrada respecto de la masa de flujo de salida en un tubo Venturi, necesariamente debe aumentar la caída de la presión a nivel de la constricción. Entonces, cuando aumenta el delta de presión de entrada y salida y además aumenta el radio de contracción, también aumentará la masa de flujo[26]. Los mismos autores proponen que para un radio de contracción entre 0,25 – 0,55 m, la presión cae entre 60 a 83 kilopascales (KPa). El pascal (Pa) es la unidad de presión del Sistema Internacional de Unidades y se define como la presión que ejerce una fuerza de 1 Newton sobre una superficie de 1 metro cuadrado. Cuando el número de Reynolds es mayor a 2.000 y el radio de expansión es mayor a 1,4 (incremento del radio de expansión) el flujo se distribuye asimétricamente en el tubo Venturi[27].
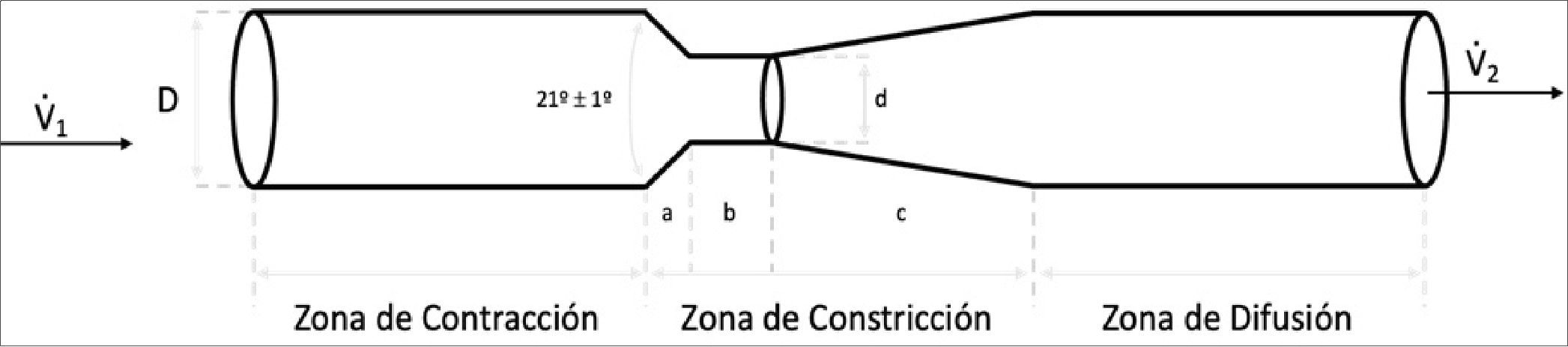
Figura 5. Diagrama estructural de un tubo Venturi. V1: Flujo de entrada, V2: Flujo de salida, D: Diámetro de entrada en la zona de contracción; a: zona convergente, b: constricción, c: zona divergente, d: Diámetro de salida en la zona de constricción.
Zhang et al[28], realizó un análisis numérico basado en “software” que simuló flujo y presiones en un tubo Venturi bajo distintas variaciones en el diagrama estructural. Entre las conclusiones de su trabajo, destaca que la relación entre el radio y el largo de la zona de constricción afecta sutilmente a la velocidad del flujo, y que la relación entre el radio y el largo de la zona de constricción afecta sutilmente el grado de succión y la masa de flujo[29]. Concluyeron además que la variabilidad de la presión generada ocurre en la transición entre la zona de contracción y la zona de constricción.
Los principales parámetros estructurales que afectan la distribución de la presión en el tubo Venturi son: el radio de la zona de contracción, el ángulo de difusión y la diferencia de presión entre la entrada y la salida del sistema.
El grado de succión que se produce dentro del tubo Venturi, muestra una variación lineal negativa en relación con la zona de contracción y al ángulo de la zona de difusión. Es decir, a mayor radio en la zona de contracción, mayor será el grado de succión y mayor será el flujo de masa entrante.
A medida que aumenta el ángulo en la zona de difusión, disminuyen tanto el grado de succión como el flujo de masa.
Cuando el radio de la zona de contracción es inferior a 0,2 o el ángulo de la zona de difusión es inferior a 35°, la velocidad tiene una distribución asimétrica en el tubo Venturi.
Tradicionalmente se ha propuesto el uso de inyectores de oxígeno como dispositivos capaces de generar alto flujo (> 30 L/min) y presión positiva ante resistencias frecuentes del ámbito clínico (máscaras) en condiciones de flujo y presiones en sistemas estables, sin haber sido valorado su rendimiento comparativo respecto a un tubo Venturi. Maturana et al[30] compararon flujos, presiones y concentración de oxígeno ante resistencias clínicas de uso frecuente: inyectores de máscaras de oxígeno y tubos Venturi comercialmente disponibles.
Los autores realizaron un estudio “wench work” comparando 225 mediciones seriadas y repetidas entre los inyectores de máscara Multivent®, tubos Venturi Dimar® y sistemas Hsiner®. Midieron flujos, presiones y concentración de O2 mediante el uso del dispositivo Citrex H4® (IMT Analytics, Suiza) y compararon flujos de ingreso de oxígeno entre 3 y 15 L/min para cada dispositivo en distintos escenarios.
Los autores encontraron flujos totales medidos de 85,6 L/ min para el sistema Venturi Dimar®; de 14,1 L/m para Multi- vent®; y de 8,4 L/m para Hsiner®.
La FiO2 total de las mediciones fue de 36,8% para Venturi Dimar®; de 58% para Multivent® y 60,9 % para Hsiner®.
Con respecto a las presiones, para el sistema Venturi Dimar® midieron 6,1 mbar; para Multivent® midieron 0,5 mbar; y para Hsiner® midieron 0,4 mbar (Figura 6).
Concluyeron, que los sistemas de inyector de O2 Multivent® y Hsiner® no entregan presión positiva en ningún escenario experimental, mientras que el tubo Venturi Dimar® entrega 1,7 mbar por litro/minuto programado.
Un aumento en la resistencia se traduce en una disminución del flujo en todos los sistemas.
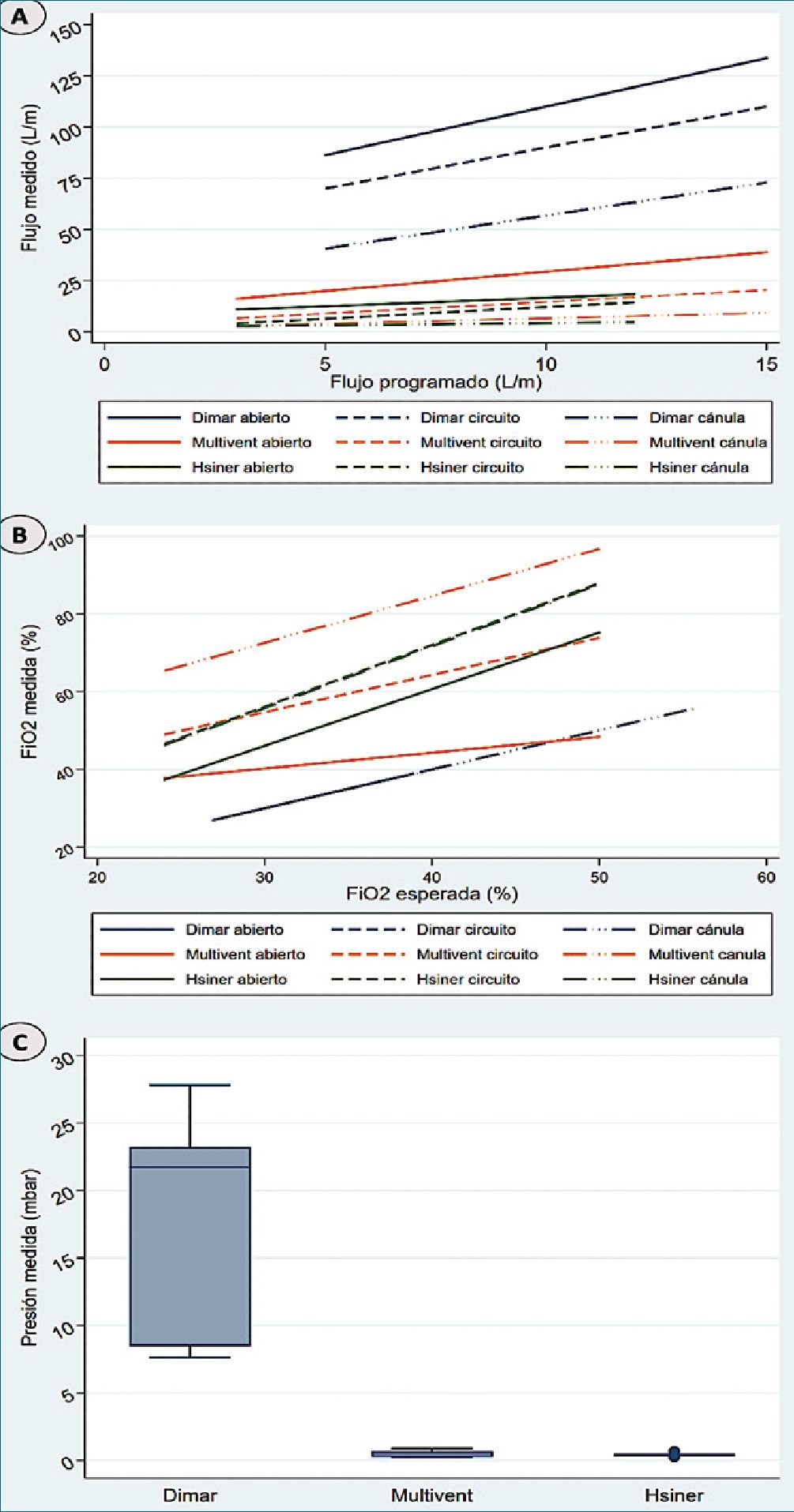
Figura 6. A) Comparación de flujo programado vs medido entre los distintos inyectores de máscara, B) Comparación de FiO2 esperada vs medida entre los distintos inyectores de máscara, C) Comparación de medición de presiones entre los distintos inyectores de máscara.
A mayor resistencia clínica, menor FiO2 (5,8% para Dimar®, basal de 25%; 17,4% para Multivent®, basal de 23,7%; y 52% para Hsiner®, basal del 50%) suponiendo estancamiento del gas ante resistencia, lo cual se traduce en menor presión y flujo post sistema, aunque con un aumento de la FiO2 (Figura 6).
El uso clínico de dispositivos de oxigenoterapia de alto flujo es actualmente una herramienta fundamental en el manejo y soporte ventilatorio para los pacientes hipoxémicos. Sin embar
go, es trascendental entender el concepto físico y dinámico del funcionamiento de cada uno de estos dispositivos para saber cuál es el más adecuado a utilizar según la demanda de cada paciente.
El mecanismo de funcionamiento de una mascarilla Venti- mask® o Multivent® se basa en el principio de Bernoulli (modificado); pero no cumple los requisitos estructurales de diseño para atribuirse la denominación de Venturi al ser un sistema modificado y abierto en términos de post restricción.
Un real tubo Venturi, es un complejo sistema aerodinámico que aplica conceptos geométricos, físicos y termodinámicos. Su funcionamiento se argumenta en el principio de Bernoulli, el cual describe a una masa de flujo entrante (oxígeno) que avanza hacia una zona interna de constricción (menor radio) provocando un aumento de la velocidad de transición del oxígeno y además una caída de su presión, lo cual por ende genera un efecto de succión que permite incorporar aire ambiental al flujo. El flujo final (mezcla), una vez superada la zona de constricción, recupera su presión y velocidad iniciales proporcionando una FiO2 predecible y controlada.
El diseño estructural de un real tubo Venturi, según la Norma ISO, consta de una zona de entrada del flujo o zona de contracción (convergente) la misma que cuenta con una angu- lación de 21° ± 1°; una zona de constricción por acortamiento del diámetro que a su vez incluye una apertura que permite la incorporación de un flujo externo (aire ambiental) y finalmente una zona de difusión (divergente) con una angulación de entre 7° y 15°.
Los sistemas de inyector de O2 tipo “jet” son capaces de generar alto flujo y FiO2 predecibles siempre que no se expongan a una resistencia. Sin embargo, en la actualidad, ninguna mascarilla de oxigenoterapia cuenta con un adecuado diseño mecánico que cumpla las especificaciones estructurales de un tubo Venturi, y por lo tanto, ninguna otorga este beneficio.
Financiación: El presente manuscrito no ha recibido financiación alguna.
Conflicto de intereses: Ninguno de los autores reconoce conflicto de intereses con el actual manuscrito.
Referencias
1. Fajardo A, Medina A, Modesto V, Gordo-Vidal F. El lado oculto de la hipoxemia. Rev Chil Anest. 2020;49(6):784–95. https://doi.org/10.25237/revchilanestv49n06-04.
2. Grensemann J, Sakka S, Pastene B, Leone M, Ferrari S, Isirdi A, et al. Oxygen : Too Much is Bad. ICU Manag Pract. 2021;21(3):130–2.
3. Austin MA, Wills KE, Blizzard L, Walters EH, Wood-Baker R. Effect of high flow oxygen on mortality in chronic obstructive pulmonary disease patients in prehospital setting: randomised controlled trial. BMJ. 2010 Oct;341(7779):c5462. https://doi.org/10.1136/bmj.c5462 PMID:20959284
4. Kumar VH, Chaker El Khoury J, Gronostajski R, Wang H, Nielsen L, Ryan RM. Nfib hemizygous mice are protected from hyperoxic lung injury and death [Internet]. Physiol Rep. 2017 Aug;5(16):e13398. https://doi.org/10.14814/phy2.13398 PMID:28830981
5. Davis WB, Rennard SI, Bitterman PB, Crystal RG. Pulmonary oxygen toxicity. Early reversible changes in human alveolar structures induced by hyperoxia [Internet]. N Engl J Med. 1983 Oct;309(15):878–83. https://doi.org/10.1056/NEJM198310133091502 PMID:6888481
6. Jones RC, Capen DE. Alveolar oxygen tension and angio-architecture of the distal adult lung [Internet]. Ultrastruct Pathol. 2013 Dec;37(6):395–407. https://doi.org/10.3109/01913123.2013.831156 PMID:24144043
7. Bajpai P. Chapter 23 – Hydraulics. In: Bajpai P, editor. Biermann’s Handbook of Pulp and Paper (Third Edition) [Internet]. Third Edit. Elsevier; 2018. p. 455–82. Available from: https://www.sciencedirect.com/science/article/pii/B9780128142387000234
8. Tavamani JP. Research Article Bernoulli Equation in Fluid Flow. Int J Curr Res. 2016;2(10):2–4.
9. Synolakis CE, Badeer HS. On combining the Bernoulli and Poiseuille equation-A plea to authors of college physics texts. Am J Phys. 1989;57(11):1013–9. https://doi.org/10.1119/1.15812.
10. Davis P, Kenny G. Basic Physics and Measurement in Anaesthesia. 5th ed. Edinburgh: Butterworth Heinemann; 2003. pp. 19–20.
11. Jennings SG. The mean free path in air. J Aerosol Sci. 1988;19(2):159–66. https://doi.org/10.1016/0021-8502(88)90219-4.
12. Kleinstreuer C. Modern Fluid Dynamics. Springer; 2010. https://doi.org/10.1007/978-1-4020-8670-0.
13. Jones NL. Moran Campbell, 1925–2004. Am J Respir Crit Care Med. 2004;170(3):222–222. https://doi.org/10.1164/rccm.2406001.
14. Patel BK, Wolfe KS, Pohlman AS, Hall JB, Kress JP. Effect of noninvasive ventilation delivered by helmet vs face mask on the rate of endotracheal intubation in patients with acute respiratory distress syndrome a randomized clinical trial. JAMA -. JAMA. 2016 Jun;315(22):2435–41. https://doi.org/10.1001/jama.2016.6338 PMID:27179847
15. Ball L, Lumb AB, Pelosi P. Intraoperative fraction of inspired oxygen: bringing back the focus on patient outcome. Br J Anaesth. 2017 Jul;119(1):16–8. https://doi.org/10.1093/bja/aex176 PMID:28974078
16. Samuel R. OBITUARY. 2004;11(4):271–3.
17. George R. Light, R.Matthay M. Chest medicine: essentials of pulmonary and critical care medicine. 5th ed. Philadelphia: Lippincott, Williams & Wilkins; 2005.
18. Adcock CJ, Dawson JS. The Venturi mask: more than moulded plastic. Br J Hosp Med (Lond). 2007 Feb;68(2):M28–9. https://doi.org/10.12968/hmed.2007.68.Sup2.22841 PMID:17370710
19. Scacci R. Air entrainment masks: jet mixing is how they work; the Venturi and Bernoulli principles are how they don’t. Respir Care. 1979;24:928–31.
20. Kittredge P. Neither venturi nor Bernoulli. Lancet. 1983 Jan;1(8317):182. https://doi.org/10.1016/S0140-6736(83)92779-4 PMID:6130219
21. Miller R. Miller’s Anesthesia. 6th ed. Philadelphia: Elsevier Churchill Livingstone; 2005. pp. 1202–3.
22. Wang XJ, Tang L, Jiang Z. Numerical simulation of Venturi ejector reactor in yellow phosphorus purification system [Internet]. Nucl Eng Des. 2014;268:18–23. https://doi.org/10.1016/j.nucengdes.2013.11.083.
23. Rodio MG, Congedo PM. Robust analysis of cavitating flows in the Venturi tube [Internet]. Eur J Mech BFluids. 2014;44:88–99. https://doi.org/10.1016/j.euromechflu.2013.11.002.
24. Gupta B, Nayak AK, Kandar TK, Nair S. Investigation of air-water two phase flow through a venturi [Internet]. Exp Therm Fluid Sci. 2016;70:148–54. https://doi.org/10.1016/j.expthermflusci.2015.07.012.
25. Sun Y, Niu W. Effects of Venturi structural parameters on the hydraulic performance. J Northwest A F Uni. 2010;38(2):211–218.
26. Qi L, Chen L. Numerical research on the hydraulic characteristics of venturi tube based on ANSYS-CFX. Tech Super Pet Ind. 2014;(6):41–5.
27. Shen S, Yang M, Jiang Y, Wang Y. The numerical simulation of the influence of Venturi burner’s structure on rich/lean separation. J Eng Thermophys. 2015;36(2):347–50.
28. Zhang JX. Analysis on the effect of venturi tube structural parameters on fluid flow [Internet]. AIP Adv. 2017;7(6):065315. https://doi.org/10.1063/1.4991441.
29. Tukimin A, Zuber M, Ahmad KA. CFD analysis of flow through Venturi tube and its discharge coefficient. IOP Conf Ser Mater Sci Eng. 2016;152(1):0–8. https://doi.org/10.1088/1757-899X/152/1/012062.
30. Maturana M, Adasme R. Comparación de rendimiento neumático ante resistencias clínicamente frecuentes entre inyectores de máscaras de oxígeno y tubos Venturi comercialmente disponibles. Med Intensiva Chile. 2020;35(4):trabajos libres.

 ORCID
ORCID